题目内容
房间里有n盏电灯,分别由n个开关控制,至少开1盏灯用以照明,共有an种不同的照明方法(其中n∈N*)
(1)当n=5时,求a5;
(2)求an;
(3)求证:
+
+…+
<1.
(1)当n=5时,求a5;
(2)求an;
(3)求证:
| 1 |
| a1+1 |
| 1 |
| 2(a2+1) |
| 1 |
| n(an+1) |
考点:二项式定理的应用
专题:综合题,二项式定理
分析:(1)a5表示房间里有5个开关控制,至少开1盏灯用以照明的照明方法;
(2)利用间接法,可求an;
(3)利用放缩法,结合等比数列的求和公式可得结论.
(2)利用间接法,可求an;
(3)利用放缩法,结合等比数列的求和公式可得结论.
解答:
(1)解:a5=
+
+
+
+
=31; (2分)
(2)解:an=
+
+…+
=2n-1; (6分)
(3)证明:因为
=
≤
,
所以
+
+…
<
+
+
+…+
=
<1(14分)
| C | 1 5 |
| C | 2 5 |
| C | 3 5 |
| C | 4 5 |
| C | 5 5 |
(2)解:an=
| C | 1 n |
| C | 2 n |
| C | n n |
(3)证明:因为
| 1 |
| n(an+1) |
| 1 |
| n•2n |
| 1 |
| 2n |
所以
| 1 |
| a1+1 |
| 1 |
| 2(a2+1) |
| 1 |
| n(an+1) |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| ||||
1-
|
点评:本题考查二项式定理的应用,考查等比数列的求和公式,正确运用组合知识是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
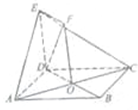 如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=
如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=