题目内容
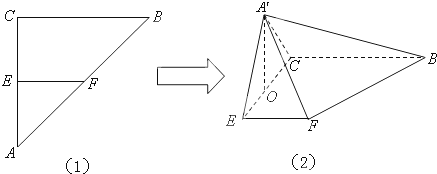
如图（1），△ABC是等腰直角三角形，其中AC=BC=4，E，F分别为AC，AB的中点，将△AEF沿EF折起，点A的位置变为点A′，已知点A′在平面BCEF上的射影O为EC的中点，如图（2）所示．
（Ⅰ）求证：EF⊥A′C；
（Ⅱ）求三棱锥F-A'BC的体积．
（Ⅰ）求证：EF⊥A′C；
（Ⅱ）求三棱锥F-A'BC的体积．
考点：棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：（Ⅰ）由已知得EF⊥AC，EF⊥A′E，EF⊥EC，从而EF⊥平面A′EC，由此能证明EF⊥A′C．
（Ⅱ）由VF-A′BC=VA′-FBC，利用等积法能求出三棱锥F-A′BC的体积．
（Ⅱ）由VF-A′BC=VA′-FBC，利用等积法能求出三棱锥F-A′BC的体积．
解答：
（Ⅰ）证明：在△ABC中，EF是等腰直角三角形ABC的中位线，
∴EF⊥AC，
在四棱锥A′-BCEF中，EF⊥A′E，EF⊥EC，
∴EF⊥平面A‘EC，
∴EF⊥A′C．
（Ⅱ）解：在直角梯形EFBC中，
EC=2，BCS△FBC=
BC×EC=4，
又∵A′O垂直平分EC，∴A′O=
=
，
∴三棱锥F-A'BC的体积：
VF-A′BC=VA′-FBC=
S△FBC•A′O=
×4×
=
．
∴EF⊥AC，
在四棱锥A′-BCEF中，EF⊥A′E，EF⊥EC，
∴EF⊥平面A‘EC，
∴EF⊥A′C．
（Ⅱ）解：在直角梯形EFBC中，
EC=2，BCS△FBC=
| 1 |
| 2 |
又∵A′O垂直平分EC，∴A′O=
| A′E2-EO2 |
| 3 |
∴三棱锥F-A'BC的体积：
VF-A′BC=VA′-FBC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
点评：本题考查异面直线垂直的证明，考查三棱锥的体积的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目