题目内容
13.已知函数f(x)=lnx.(1)求函数g(x)=f(x)+mx2-4x在定义域内单调递增,求实数m的取值范围;
(2)若b>a>0,求证:f(b)-f(a)>$\frac{2ab-2{a}^{2}}{{a}^{2}+{b}^{2}}$.
分析 (1)g(x)=f(x)+mx2-4x=lnx+mx2-4x在定义域内单调递增,只需g′(x)≥0在(0,+∞)上单调递增,即可求实数m的取值范围.
(2)欲证f(b)-f(a)>$\frac{2ab-2{a}^{2}}{{a}^{2}+{b}^{2}}$,即证$lnb-lna=ln\frac{b}{a}>\frac{2ab-2{a}^{2}}{{a}^{2}+{b}^{2}}=\frac{2(\frac{b}{a})-2}{1+(\frac{b}{a})^{2}}$
令$t=\frac{b}{a}>1$,即证lnt>$\frac{2t-2}{1+{t}^{2}}$,即证(1+t2)lnt>2t-2当t>1时恒成立
构造函数F(t)=(1+t2)lnt-2t+2即可.
解答 解:(1)g(x)=f(x)+mx2-4x=lnx+mx2-4x (x>0)
则g′(x)$\frac{1}{x}+2mx-4$≥0在(0,+∞)上恒成立,即2m≥$\frac{4}{x}-\frac{1}{{x}^{2}}$恒成立
∵$\frac{4}{x}-\frac{1}{{x}^{2}}=-(\frac{1}{x}-2)^{2}+4≤4$∴m≥2.
(2)欲证f(b)-f(a)>$\frac{2ab-2{a}^{2}}{{a}^{2}+{b}^{2}}$,即证$lnb-lna=ln\frac{b}{a}>\frac{2ab-2{a}^{2}}{{a}^{2}+{b}^{2}}=\frac{2(\frac{b}{a})-2}{1+(\frac{b}{a})^{2}}$
令$t=\frac{b}{a}>1$,即证lnt>$\frac{2t-2}{1+{t}^{2}}$,即证(1+t2)lnt>2t-2当t>1时恒成立
构造函数F(t)=(1+t2)lnt-2t+2
求导$F′(t)=2tlnt+t+\frac{1}{t}-2$
∵t>1∴2tlnt>0,∵$t+\frac{1}{t}-2>0$,所以F′(t)>0当t>1时恒成立
所以F(t)在(1,+∞)单调递增
所以F(t)>F(1)=0恒成立.
故不等式(1+t2)lnt>2t-2得证,所以f(b)-f(a)>$\frac{2ab-2{a}^{2}}{{a}^{2}+{b}^{2}}$.成立.
点评 本题考查了已知单调性,求参数取值的基本方法,同时考查了证明函数不等式的构造新函数法,属于难题.

 名校课堂系列答案
名校课堂系列答案| A. | 公差为1的等差数列 | B. | 公差为$\frac{1}{3}$的等差数列 | ||
| C. | 公差为-$\frac{1}{3}$的等差数列 | D. | 不是等差数列 |
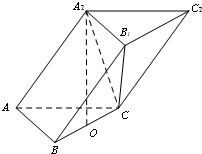 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=$\sqrt{5}$,BC=4,BC的中点为O,A1O垂直于底面ABC.
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=$\sqrt{5}$,BC=4,BC的中点为O,A1O垂直于底面ABC.