题目内容
8.已知椭圆E的中心在原点,焦点在坐标轴上,且经过两点M(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)和N(1,$\frac{\sqrt{2}}{2}$).(1)求椭圆E的方程;
(2)设点F($\frac{\sqrt{2}}{3}$,0),过点F作直线l交椭圆E于AB两点,以AB为直径的圆交y轴于P、Q两点,劣弧长PQ记为d,求$\frac{d}{|AB|}$的最大值.
分析 (1)不妨设椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),半焦距为c.由已知条件,$\left\{\begin{array}{l}{\frac{1}{2{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\end{array}\right.$,解出即可得出.
(2)由点F($\frac{\sqrt{2}}{3}$,0),设A(x1,y1),B(x2,y2).设直线l方程为:my=x-$\frac{\sqrt{2}}{3}$,联立直线与椭圆方程,消去x整理可知:(m2+2)y2+$\frac{2\sqrt{2}m}{3}y$-$\frac{16}{9}$=0,AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,可得线段AB的中点T,⊙T的半径为r=$\frac{1}{2}$|AB|.经过点T作TE⊥y轴,垂足为E,设∠QTE=θ∈$(0,\frac{π}{2})$.$\frac{d}{|AB|}$=θ,计算cosθ=$\frac{{x}_{T}}{\frac{1}{2}|AB|}$,利用函数的单调性进而得出.当AB与x轴重合时,AB与椭圆的长轴重合.
解答 解:(1)不妨设椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),半焦距为c.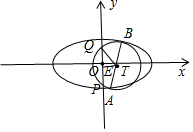
由已知条件,$\left\{\begin{array}{l}{\frac{1}{2{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\end{array}\right.$,
解得a2=2,b=1.
∴椭圆E的方程为:$\frac{{x}^{2}}{2}$+y2=1.
(2)由点F($\frac{\sqrt{2}}{3}$,0),设A(x1,y1),B(x2,y2).
设直线l方程为:my=x-$\frac{\sqrt{2}}{3}$,
联立直线与椭圆方程,消去x整理可知:(m2+2)y2+$\frac{2\sqrt{2}m}{3}y$-$\frac{16}{9}$=0,
∴y1+y2=$\frac{-2\sqrt{2}m}{3({m}^{2}+2)}$,y1y2=$\frac{-16}{9({m}^{2}+2)}$.
|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\frac{2\sqrt{(1+{m}^{2})(18{m}^{2}+32)}}{3({m}^{2}+2)}$,
则线段AB的中点T$(\frac{2\sqrt{2}}{3{m}^{2}+6},\frac{-\sqrt{2}m}{3{m}^{2}+6})$,⊙T的半径为r=$\frac{1}{2}$|AB|.
经过点T作TE⊥y轴,垂足为E,设∠QTE=θ∈$(0,\frac{π}{2}]$.
则$\frac{d}{|AB|}$=$\frac{r•2θ}{2r}$=θ,
cosθ=$\frac{{x}_{T}}{\frac{1}{2}|AB|}$=$\frac{2{x}_{T}}{|AB|}$=$\frac{2\sqrt{2}}{\sqrt{(1+{m}^{2})(18{m}^{2}+32)}}$,
令m2=t≥0,g(t)=(1+t)(18t+32)=18t2+50t+32≥32,
∴cosθ≤$\frac{2\sqrt{2}}{\sqrt{32}}$=$\frac{1}{2}$,∴θ∈$[\frac{π}{3},\frac{π}{2})$.
当AB与x轴重合时,AB与椭圆的长轴重合,此时劣弧长PQ=πr,则$\frac{d}{|AB|}$=$\frac{π}{2}$.
综上可得:$\frac{d}{|AB|}$的最大值为$\frac{π}{2}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、函数的单调性,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -1 | D. | 1 |
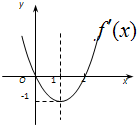 已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)
已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)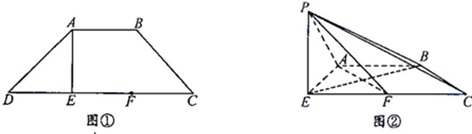
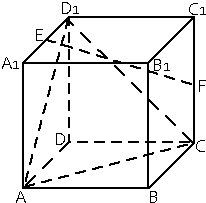 如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.
如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.