题目内容
5.已知函数$f(x)=2sin(\frac{x}{2}+\frac{π}{3}),x∈R$.(1)求它的周期;
(2)求f(x)最大值和此时相应的x的值;
(3)求f(x)的单调增区间.
分析 (1)由解析式和三角函数的周期公式求出函数的周期;
(2)由正弦函数的最大值和整体思想求出答案;
(3)由正弦函数的增区间和整体思想,求出f(x)的单调增区间.
解答 解:(1)由题意得,T=$\frac{2π}{\frac{1}{2}}$=4π,
∴函数f(x)的周期是4π;
(2)当$in(\frac{x}{2}+\frac{π}{3})=1$ 时,f(x)取到最大值是f(x)max=2,
此时$\frac{x}{2}+\frac{π}{3}=\frac{π}{2}+2kπ$(k∈Z),解得$x=\frac{π}{3}+4kπ,k∈z$;
(3)由$-\frac{π}{2}+2kπ≤\frac{x}{2}+\frac{π}{3}≤\frac{π}{2}+2kπ(k∈Z)$得,
$-\frac{5π}{3}+4kπ≤x≤\frac{π}{3}+4kπ,k∈z$,
∴f(x)的单调增区间是$[-\frac{5π}{3}+4kπ,\frac{π}{3}+4kπ](k∈z)$.
点评 本题考查了由正弦函数的增区间、最值,以及三角函数的周期公式,考查整体思想,化简、计算能力.

练习册系列答案
相关题目
15.已知函数f(x)=x3+ax2+bx在x=1处有极值10,则f(2)等于( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
16.已知f(x)=($\frac{1}{3}$)x-log3x,实数a、b、c满足f(a)•f(b)•f(c)<0,且0<a<b<c,若实数x0是函数f(x)的一个零点,那么下列不等式中,不可能成立的是( )
| A. | x0<a | B. | x0>b | C. | x0<c | D. | x0>c |
14.设函数f(x)=ex(sinx-cosx)(0≤x≤2015π)的极小值点的个数为( )
| A. | 1007 | B. | 1008 | C. | 2015 | D. | 2016 |
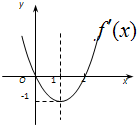 已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)
已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)