题目内容
已知f(x)=aln(x-1),g(x)=x2+bx,F(x)=f(x+1)-g(x),其中a,b∈R.
(I)若y=f(x)与y=g(x)的图象在交点(2,k)处的切线互相垂直,求a,b的值;
(Ⅱ)当b=2-a,a>0时,求F(x)的最大值;
(Ⅲ)若x=2是函数F(x)的一个极值点,x0和1是F(x)的两个零点,且x0∈(n,n+1),n∈N,求n.
(I)若y=f(x)与y=g(x)的图象在交点(2,k)处的切线互相垂直,求a,b的值;
(Ⅱ)当b=2-a,a>0时,求F(x)的最大值;
(Ⅲ)若x=2是函数F(x)的一个极值点,x0和1是F(x)的两个零点,且x0∈(n,n+1),n∈N,求n.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)根据导数的几何意义建立切线斜率之间的关系建立方程,求a,b的值;
(Ⅱ)利用导数判断函数的单调性求出最大值;
(Ⅲ)根据导数和函数极值之间的关系建立方程,即可求n;
(Ⅱ)利用导数判断函数的单调性求出最大值;
(Ⅲ)根据导数和函数极值之间的关系建立方程,即可求n;
解答:
解:(I)f′(x)=
,g'(x)=2x+b…(1分)
由题知
,即
…(2分)
解得a=-
,b=-2.
(Ⅱ)当b=2-a时,F(x)=alnx-[x2+(2-a)x],
∴F′(x)=
-2x-(2-a)=
=
,----------------(6分)
∵a>0,∴
>0,又x>0,x+1>0,
则由F′(x)=0,解得x=
,-------------------------------------(7分)
F(x)与F′(x)的变化情况如下表:
∴F(x)max=F(
)=aln
-[
+(2-a)•
]=aln
+
-a.--------------------(9分)
(Ⅲ)F(x)=f(x+1)-g(x)=alnx-(x2+bx),F′(x)=
-2x-b
由题知
,即
,即解得a=6,b=-1…(11分)
∴F(x)=6lnx-(x2-x),F′(x)=
-2x+1=
,
∵x>0,由F'(x)>0,解得0<x<2;由F'(x)<0,解得x>2
∴F(x)在(0,2)上单调递增,在(2,+∞)单调递减,
故F(x)至多有两个零点,其中x1∈(0,2),x2∈(2,+∞)…(12分)
又F(2)>F(1)=0,F(3)=6(ln3-1)>0,F(4)=6(ln4-2)<0
∴x0∈(3,4),故n=3 …(14分)
| a |
| x-1 |
由题知
|
|
解得a=-
| 1 |
| 2 |
(Ⅱ)当b=2-a时,F(x)=alnx-[x2+(2-a)x],
∴F′(x)=
| a |
| x |
| a-2x2-(2-a)x |
| x |
| (2x-a)(x+1) |
| x |
∵a>0,∴
| a |
| 2 |
则由F′(x)=0,解得x=
| a |
| 2 |
F(x)与F′(x)的变化情况如下表:
| x | (0,
|
|
(
| ||||||
| F′(x) | + | 0 | - | ||||||
| F(x) | ↗ | 极大值 | ↘ |
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
(Ⅲ)F(x)=f(x+1)-g(x)=alnx-(x2+bx),F′(x)=
| a |
| x |
由题知
|
|
∴F(x)=6lnx-(x2-x),F′(x)=
| 6 |
| x |
| -(2x+3)(x-2) |
| x |
∵x>0,由F'(x)>0,解得0<x<2;由F'(x)<0,解得x>2
∴F(x)在(0,2)上单调递增,在(2,+∞)单调递减,
故F(x)至多有两个零点,其中x1∈(0,2),x2∈(2,+∞)…(12分)
又F(2)>F(1)=0,F(3)=6(ln3-1)>0,F(4)=6(ln4-2)<0
∴x0∈(3,4),故n=3 …(14分)
点评:本题主要考查导数的应用,要求熟练掌握函数的性质和导数之间的关系,考查学生的运算能力.

练习册系列答案
相关题目
在曲线y=x2的切线的倾斜角为
的点为( )
| 3π |
| 4 |
| A、(0,0) | ||||||||
B、(
| ||||||||
C、(-
| ||||||||
D、(
|
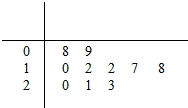 现从某100件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,
现从某100件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,