题目内容
19.对函数f(x)=$\frac{cosx+m}{cosx+2}$,若?a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )| A. | $(\;\frac{5}{4}\;,\;6\;)$ | B. | $(\;\frac{5}{3}\;,\;6\;)$ | C. | $(\;\frac{7}{5}\;,\;5\;)$ | D. | $(\;\frac{5}{4}\;,\;5\;)$ |
分析 当m=2时,f(a)=f(b)=f(c)=1,是等边三角形的三边长;当m>2时,只要$2(1+\frac{m-2}{3})>m-1$即可,当m<2时,只要$1+\frac{m-2}{3}<2(m-1)$即可,由此能求出结果.
解答 解:当m=2时,f(x)=$\frac{cosx+2}{cosx+2}$=1,
此时f(a)=f(b)=f(c)=1,是等边三角形的三边长,成立;
当m>2时,$f(x)∈[1+\frac{m-2}{3},m-1]$,
只要$2(1+\frac{m-2}{3})>m-1$即可,解得2<m<5;
当m<2时,$f(x)∈[m-1,1+\frac{m-2}{3}]$,
只要$1+\frac{m-2}{3}<2(m-1)$即可,
解得$\frac{7}{5}<m<2$,
综上$m∈(\frac{7}{5},5)$.
故选:C.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
14.已知集合A={x|x2-2x-3<0},$B=\{\;x|\frac{1}{x}<1\;\}$,则A∩B=( )
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<0或0<x<3} | D. | {x|-1<x<0或1<x<3} |
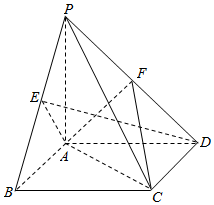 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.