题目内容
已知f(x)=x
(n∈Z)的图象在[0,+∞)上单调递增,解不等式f(x2-x)>f(x+3)
| 1 |
| -n2+2n+3 |
考点:幂函数的性质
专题:函数的性质及应用,不等式的解法及应用
分析:根据题意,求出n的值,讨论n的取值对应的函数f(x)的单调性,求出不等式f(x2-x)>f(x+3)的解集来.
解答:
解:根据题意,
>0,
即-n2+2n+3>0,
解得-1<n<3;
又∵n∈Z,
∴n=0,1,2;
当n=0时,f(x)=x
,
当n=1时,f(x)=x
,
当n=2时,f(x)=x
;
∴当n=0或2时,f(x)=x
,函数在R上单调递增,
∵f(x2-x)>f(x+3),
∴x2-x>x+3,
解得x<-1或x>3,
∴原不等式的解集为(-∞,-1)∪(3,+∞);
当n=1时,f(x)=x
,函数在[0,+∞)上单调递增,
∵f(x2-x)>f(x+3),
∴
,
解得-3≤x<-1或x>3,
∴原不等式的解集为[-3,-1)∪(3,+∞).
| 1 |
| -n2+2n+3 |
即-n2+2n+3>0,
解得-1<n<3;
又∵n∈Z,
∴n=0,1,2;
当n=0时,f(x)=x
| 1 |
| 3 |
当n=1时,f(x)=x
| 1 |
| 4 |
当n=2时,f(x)=x
| 1 |
| 3 |
∴当n=0或2时,f(x)=x
| 1 |
| 3 |
∵f(x2-x)>f(x+3),
∴x2-x>x+3,
解得x<-1或x>3,
∴原不等式的解集为(-∞,-1)∪(3,+∞);
当n=1时,f(x)=x
| 1 |
| 4 |
∵f(x2-x)>f(x+3),
∴
|
解得-3≤x<-1或x>3,
∴原不等式的解集为[-3,-1)∪(3,+∞).
点评:本题考查了幂函数的性质与应用的问题,也考查了不等式的解法与应用问题,解题时容易忽略第一个条件,直接去研究如何解不等式,题目中给出的所有条件都是对题目的诠释,是综合题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
如果不等式组
表示的平面区域是一个直角三角形,则实数k的值为( )
|
A、-
| ||
| B、0 | ||
C、
| ||
D、0或-
|
观察如图:

若第n行的各数之和等于20112,则n=( )

若第n行的各数之和等于20112,则n=( )
| A、2011 | B、2012 |
| C、1006 | D、1005 |
| 5 | a-2 |
A、a -
| ||
B、a
| ||
C、a
| ||
D、-a
|
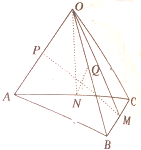 如图,已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC,求证:PM⊥QN.
如图,已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC,求证:PM⊥QN.