题目内容
已知函数f(x)=cos2x+sinx,x∈[-
,
]的值域.
| π |
| 4 |
| π |
| 4 |
考点:三角函数的最值
专题:三角函数的求值
分析:根据函数f(x)=cos2x+sinx=-(sinx-
)2+
,sinx∈[-
,
],再利用二次函数的性质求得f(x)的值域.
| 1 |
| 2 |
| 5 |
| 4 |
| ||
| 2 |
| ||
| 2 |
解答:
解:∵函数f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-
)2+
,当x∈[-
,
]时,sinx∈[-
,
],
故当sinx=-
时,f(x)取得最小值为
,当sinx=
时,f(x)取得最大值为
,
故函数的值域为[
,
].
| 1 |
| 2 |
| 5 |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
故当sinx=-
| ||
| 2 |
1-
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
故函数的值域为[
1-
| ||
| 2 |
| 5 |
| 4 |
点评:本题主要考查二次函数的性质,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
“x-1≠0”是“(x-1)(x-2)≠0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既不充分也非必要条件 |
已知函数f(x)=sinωx+cosωx,如果存在实数x1,使得对任意的实数x,都有f(x1)≤f(x)≤f(x1+2010)成立,则ω的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图为函数f(x)=
如图为函数f(x)=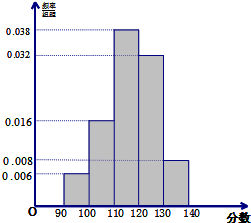 某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组[90,100),第二组[100,110),第五组[130,140].按上述分组方法得到的频率分布直方图如图所示.
某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组[90,100),第二组[100,110),第五组[130,140].按上述分组方法得到的频率分布直方图如图所示.