题目内容
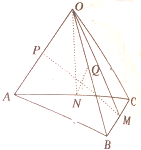如图，已知空间四边形OABC中，M为BC中点，N为AC中点，P为OA中点，Q为OB中点，若AB=OC，求证：PM⊥QN．考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：连接PQMN，利用三角形中位线的性质容易判断四边形PQMN为菱形，再由菱形的对角线性质得到所证．
解答：
证明：连接PQMN，
因为M为BC中点，N为AC中点，P为OA中点，Q为OB中点，
所以PQ∥AB，QM∥OC，MN∥AC，PN∥OC，且PQ=MN=
AB，PN=QM=
OC，
又AB=OC，
所以PQ=MN=PN=QM，
所以四边形PQMN是菱形，
所以PM⊥QN．
证明：连接PQMN，因为M为BC中点，N为AC中点，P为OA中点，Q为OB中点，
所以PQ∥AB，QM∥OC，MN∥AC，PN∥OC，且PQ=MN=
| 1 |
| 2 |
| 1 |
| 2 |
又AB=OC，
所以PQ=MN=PN=QM，
所以四边形PQMN是菱形，
所以PM⊥QN．
点评：本题考查了三角形的中位线性质以及菱形的对角线性质，属于基础题．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
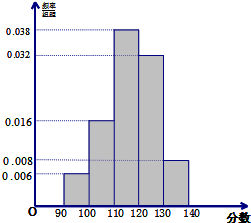某校50名学生参加2013年全国数学联赛初赛，成绩全部介于90分到140分之间．将成绩结果按如下方式分成五组：第一组[90，100），第二组[100，110），第五组[130，140]．按上述分组方法得到的频率分布直方图如图所示．“x≠2或y≠1”是“x+y≠3”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
双曲线的实轴长与虚轴长之和等于其焦距的
倍，且一个顶点的坐标为（0，2），则双曲线的标准方程为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|