题目内容
17.在△ABC中,内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且6S=(a+b)2-c2,则tanC等于( )| A. | $\frac{5}{12}$ | B. | $-\frac{5}{12}$ | C. | $\frac{12}{5}$ | D. | $-\frac{12}{5}$ |
分析 首先由三角形面积公式得到S△ABC=$\frac{1}{2}$ab•sinC,再由余弦定理,结合6S=(a+b)2-c2,得出3sinC-2cosC=2,然后通过(3sinC-2cosC)2=4,求出结果即可.
解答 解:△ABC中,∵S△ABC=$\frac{1}{2}$ab•sinC,由余弦定理:c2=a2+b2-2abcosC,且6S=(a+b)2-c2,
∴3absinC=(a+b)2-(a2+b2-2abcosC),
整理得3sinC-2cosC=2,
∴(3sinC-2cosC)2=4.
∴$\frac{(3sinC-2cosC)^{2}}{si{n}^{2}C+co{s}^{2}C}$=4,化简可得 5tan2C-12tanC=0.
∵C∈(0,180°),
∴tanC=$\frac{12}{5}$,
故选:C.
点评 本题考查了余弦定理、三角形面积公式以及三角函数的化简求值,要注意角C的范围,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.函数f(x)=2sin(ωx+φ)(w>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)+f($\frac{17π}{12}$)的值为( )
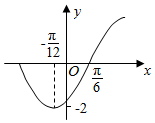
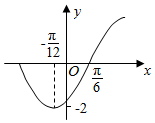
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1-$\frac{\sqrt{3}}{2}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
5.一个圆过点(-5,1)且圆心在直线2x+y+4=0上,求半径最小时的圆心坐标( )
| A. | (-1,-2) | B. | (-2,0) | C. | (-$\frac{5}{2}$,1) | D. | (-3,2) |
12.已知集合A={x|x2<1},B={x|log2x<1},则A∩B=( )
| A. | {x|-1<x<1} | B. | {x|0<x<1} | C. | {x|0<x<2} | D. | {x|-1<x<2} |
6.已知函数f(x)=ex-ax-1,g(x)=ln(ex-1)-lnx,若?x0∈(0,+∞),使得f(g(x0)>f(x0)成立,则a的取值范围是( )
| A. | (0,+∞) | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |