题目内容

20．已知函数f（x）=x3-$\frac{3}{2}{x^2}+\frac{3}{4}x+\frac{1}{8}$，则$\sum_{k=1}^{2016}{f（{\frac{k}{2017}}）}$的值为（　　）
A．0B．504C．1008D．2016

分析 使用二项式定理化简得f（x）═（x-$\frac{1}{2}$）3+$\frac{1}{4}$．根据$\frac{k}{2017}-\frac{1}{2}$与$\frac{2017-k}{2017}-\frac{1}{2}$互为相反数便可得出答案．

解答 解：f（x）=x3-$\frac{3}{2}{x^2}+\frac{3}{4}x+\frac{1}{8}$=x3-$\frac{3}{2}$x2+$\frac{3}{4}$x-$\frac{1}{8}$+$\frac{1}{4}$=（x-$\frac{1}{2}$）3+$\frac{1}{4}$．
∵$\frac{k}{2017}-\frac{1}{2}$+$\frac{2017-k}{2017}-\frac{1}{2}$=0，k=1，2，…2016．
∴（$\frac{k}{2017}$-$\frac{1}{2}$）3+（$\frac{2017-k}{2017}-\frac{1}{2}$）3=0，k=1，2，…2016．
∴$\sum_{k=1}^{2016}{f（{\frac{k}{2017}}）}$=$\frac{1}{4}×2016$=504．
故选：B．

点评 本题考查了二项式定理的应用，属于中档题．

练习册系列答案
相关题目
10．若定义域为R的函数y=f（x），其图象是连续不断的，且存在常数λ（λ∈R），使得f（x+λ）+λf（x）=0对任意实数x都成立，则称f（x）是一个“λ-伴随函数”．给出下列四个关于“λ-伴随函数”的命题：①f（x）=0是常数函数中唯一一个“λ-伴随函数”；②f（x）=x+1是“λ-伴随函数”；③f（x）=2x是“λ-伴随函数”；④当λ＞0时，“λ-伴随函数”f（x）在（0，λ）内至少有一个零点．所有真命题的序号为③．
11．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点为（0，-1），离心率e=$\frac{\sqrt{2}}{2}$．
（1）求椭圆C的方程；
（2）过M（0，m）（-1＜m＜0）的直线L交椭圆C于A、B两点，试问：在椭圆C上是否存在定点T，使得无论直线L如何转动，以AB为直径的圆恒过定点T？若存在，求出m的值及点T的坐标；若不存在，请说明理由．
8．复数z满足z（1+i）=2-i（i为虚数单位），则z的模为$\frac{\sqrt{10}}{2}$．
15．已知等比数列{an}的各项都为正数，且a3，$\frac{1}{2}{a_5}，{a_4}$成等差数列，则$\frac{{{a_3}+{a_5}}}{{{a_4}+{a_6}}}$的值是（　　）
A．$\frac{{\sqrt{5}-1}}{2}$B．$\frac{{\sqrt{5}+1}}{2}$C．$\frac{{3-\sqrt{5}}}{2}$D．$\frac{{3+\sqrt{5}}}{2}$
5．已知P={x|-4≤x≤2，x∈Z}，Q={x|-3＜x＜1}，则P∩Q=（　　）
A．（-1，3）B．[-2，1）C．{0，1，2}D．{-2，-1，0}
12．复数$\frac{2}{1+i}$的虚部是（　　）
A．-2B．-1C．1D．2
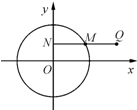6．如图，已知点M在圆O：x2+y2=4上运动，MN⊥y轴（垂足为N），点Q在NM的延长线上，且|QN|=2|MN|．
（Ⅰ）求动点Q的轨迹方程；
（Ⅱ）直线l：y=$\frac{1}{2}$x+m与（Ⅰ）中动点Q的轨迹交于两个不同的点A和B，圆O上存在两点C、D，满足|CA|=|CB|，|DA|=|DB|．
（ⅰ）求m的取值范围；
（ⅱ）求当$\frac{|CD|}{|AB|}$取得最小值时直线l的方程．
7．已知两条平行线l1：3x+4y-4=0与l2：ax+8y+2=0之间的距离是（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网