题目内容
已知a>0,函数f(x)=-2asin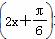 +2a+b,当x∈
+2a+b,当x∈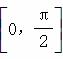 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.
(1) 求常数a、b的值;
(2) 设g(x)=f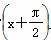 且lgg(x)>0,求g(x)的单调区间.
且lgg(x)>0,求g(x)的单调区间.
解:(1) ∵ x∈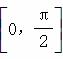 ,∴ 2x+
,∴ 2x+ ∈
∈ .
.
∴ sin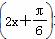 ∈
∈ ,
,
∴-2asin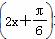 ∈[-2a,a],∴f(x)∈[b,3a+b].
∈[-2a,a],∴f(x)∈[b,3a+b].
又∵-5≤f(x)≤1,∴b=-5,3a+b=1,因此a=2,b=-5.
(2) 由(1)知a=2,b=-5,∴ f(x)=-4sin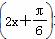 -1,
-1,
g(x)=f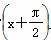 =-4sin
=-4sin -1=4sin
-1=4sin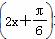 -1.
-1.
又由lgg(x)>0,得g(x)>1,∴ 4sin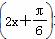 -1>1,
-1>1,
∴ sin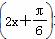 >
> ,
,
∴2kπ+ <2x+
<2x+ <2kπ+
<2kπ+ ,k∈Z.
,k∈Z.
由2kπ+ <2x+
<2x+ ≤2kπ+
≤2kπ+ (k∈Z),得g(x)的单调增区间为
(k∈Z),得g(x)的单调增区间为 (k∈Z).
(k∈Z).
由2kπ+ ≤2x+
≤2x+ <2kπ+
<2kπ+ ,得g(x)的单调减区间为
,得g(x)的单调减区间为 (k∈Z).
(k∈Z).

练习册系列答案
相关题目
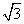 b .求角A的大小.
b .求角A的大小. <α<
<α<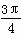 ,cos
,cos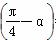 =
=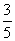 ,sin
,sin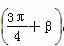 =
=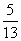 ,求sin(α+β)的值.
,求sin(α+β)的值. )的部分图象如图所示,则ω=________.
)的部分图象如图所示,则ω=________.
 个单位后,与函数y=sin
个单位后,与函数y=sin 的图象重合,则φ=________.
的图象重合,则φ=________. =
= ,且-π<α<-
,且-π<α<- ,则cos
,则cos =________.
=________. ,且角α在第四象限,计算:
,且角α在第四象限,计算: (n∈Z).
(n∈Z).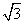 ,求直线l的方程;
,求直线l的方程;