题目内容
已知an+1+an=4n-3(n∈N*),当a1=2时,求an= .
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得an+2-an=4,a1=2,a2=-1,由此能求出an.
解答:
解:∵an+1+an=4n-3(n∈N*),
∴an+2+an+1=4n+1,
两式相减得出an+2-an=4.
∵a1=2,∴a2=4-3-2=-1
当n为奇数时,an=2+
×4=2n,
当n为偶数时,an=-1+2n.
∴an=
.
故答案为:
.
∴an+2+an+1=4n+1,
两式相减得出an+2-an=4.
∵a1=2,∴a2=4-3-2=-1
当n为奇数时,an=2+
| n-1 |
| 2 |
当n为偶数时,an=-1+2n.
∴an=
|
故答案为:
|
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意递推公式的合理运用.

练习册系列答案
相关题目
若函数f(x)唯一的一个零点同时在区间(2,16),(2,8),(2,4)内,那么下列命题中正确的是( )
| A、f(x)在区间(2,3)内有零点 |
| B、f(x)在区间(2,3)或(3,4)内有零点 |
| C、f(x)在区间(3,16)内无零点 |
| D、f(x)在区间(4,16)内无零点 |
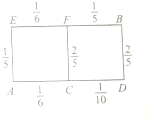 某物流公司送货员从公司A处准备开车送货到某单位B处,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D算作两个路段:路段AC发生堵车事件的概率为
某物流公司送货员从公司A处准备开车送货到某单位B处,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D算作两个路段:路段AC发生堵车事件的概率为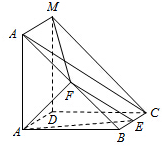 如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.
如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.