题目内容
函数f（x）=x（
+
），其中a，b∈R定义域{x|x≠0}且f（2）=
，求函数f（x）的解析表达式．
| 1 |
| 2x+b |
| 1 |
| a |
| 5 |
| 3 |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：根据函数f（x）的定义域为{x|x≠0}，得20+b=0，求出b的值；再由f（2）=
，求出a的值即可．
| 5 |
| 3 |
解答：
解：∵函数f（x）=x（
+
）的定义域为{x|x≠0}，
∴20+b=0，
解得b=-1；
又∵f（2）=
，
∴2（
+
）=
，
解得a=2；
∴函数f（x）的解析式为f（x）=x（
+
）．
| 1 |
| 2x+b |
| 1 |
| a |
∴20+b=0，
解得b=-1；
又∵f（2）=
| 5 |
| 3 |
∴2（
| 1 |
| 22-1 |
| 1 |
| a |
| 5 |
| 3 |
解得a=2；
∴函数f（x）的解析式为f（x）=x（
| 1 |
| 2x-1 |
| 1 |
| 2 |
点评：本题考查了用待定系数法求函数解析式的应用问题，是基础题目．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
已知某个几何体的三视图如图所示．根据图中标出的尺寸（单位：cm）．可得这个几何体的体积是 cm3．
（ ）
（ ）
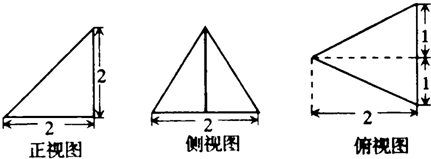
A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
从半径R的球内接正方体的8个顶点及球心这9个点中任取2个点，则这两个点间的距离小于或等于半径的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
某四棱锥的三视图如图所示，该四棱锥的表面积是（ ）
A、16+16
| ||
B、16+32
| ||
| C、48 | ||
| D、32 |