Question

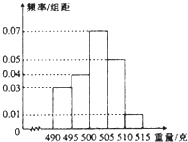某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的N件产品作为样本称出它们的重量（单位；克），重量的分组区间为（490，495]，（495，500]，…（510，515]，由此得到样本的频率分布直方图，如图所示，若其中重量超过510克的产品件数为3．
（1）求N；
（2）在抽取的重量超过505克的产品中任取2件，设ξ为重量超过510克的产品数量，求ξ的分布列及数学期望．

Answer 1

考点：离散型随机变量及其分布列,频率分布直方图,离散型随机变量的期望与方差

专题：概率与统计

分析：（Ⅰ）由题意得N×0.01×5=3，由此能求出N=60．
（Ⅱ）ξ的所有可能取值为0，1，2，重量超过505克的产品数量为60×（0.05×5+0.01×5）=18件，分别求出相应的概率，由此能求出ξ的分布列及数学期望．

解答： 解：（Ⅰ）∵重量超过510克的产品件数为3，
由频率直方图得重量超过510克的产品的频率为0.01×5=0.05．
∴由N×0.01×5=3，得N=60．
（Ⅱ）ξ的所有可能取值为0，1，2，
重量超过505克的产品数量为60×（0.05×5+0.01×5）=18件，
P（ξ=0）=

C 2 13

C 2 18

=

35

51

，
P（ξ=1）=

C 1 13 C 1 5

C 2 18

=

5

17

，
P（ξ=2）=

C 2 5

C 2 18

=

1

51

，
∴ξ的分布列为：

ξ	0	1	2
P	35 51	5 17	1 51

∴Eξ=0×

35

51

+1×

15

51

+2×

1

51

=

1

3

．

点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，是中档题．