题目内容
已知角α的终边在第四象限,且与单位圆交于P(
,y0),则
的值等于( )
| 3 |
| 5 |
| sinα+3cosα |
| 3cosα-sinα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:由条件利用任意角的三角函数的定义求得y0=-
,tanα=-
,再利用同角三角函数的基本关系求得
的值.
| 4 |
| 5 |
| 4 |
| 3 |
| sinα+3cosα |
| 3cosα-sinα |
解答:
解:由题意可得y<0,(
)2+y02=1,求得y0=-
,∴tanα=
=-
.
∴
=
=
=
,
故选:B.
| 3 |
| 5 |
| 4 |
| 5 |
| y0 | ||
|
| 4 |
| 3 |
∴
| sinα+3cosα |
| 3cosα-sinα |
| tanα+3 |
| 3-tanα |
-
| ||
3+
|
| 5 |
| 13 |
故选:B.
点评:本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
cos(
-x)=
,那么sin2x=( )
| π |
| 4 |
| 3 |
| 5 |
A、
| ||
B、±
| ||
C、-
| ||
D、
|
已知方程
+
=1(k∈R),则1<k<3是该方程表示焦点在x轴上的椭圆的( )
| x2 |
| k+1 |
| y2 |
| 3-k |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若点P在-
角的终边上,且P的坐标为(-1,y),则y等于( )
| 10π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
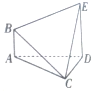 在如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AD=2,∠ACD=90°.求多面体ABEDC的体积.
在如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AD=2,∠ACD=90°.求多面体ABEDC的体积.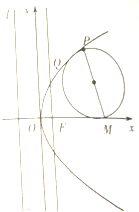 如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一点,Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为
如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一点,Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为