题目内容
10.设α,β是两个平面,m,n是两条直线,有下列四个命题:(1)如果m⊥n,m⊥α,n∥β,那么α⊥β.
(2)如果m⊥α,n∥α,那么m⊥n.
(3)如果α∥β,m?α,那么m∥β.
其中正确命题的个数( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用空间线面、面面平行与垂直的判定及其性质即可判断出正误.
解答 解:(1)如果m⊥n,m⊥α,n∥β,那么α⊥β,可能α∥β,因此不正确.
(2)如果m⊥α,n∥α,那么m⊥n,正确.
(3)如果α∥β,m?α,那么m∥β,正确.
其中正确命题的个数是2.
故选:B.
点评 本题考查了空间线面面面平行与垂直的判定及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
20.下列函数中,最小值为4的是( )
| A. | y=$\frac{lgx}{2}+\frac{8}{lgx}$ | B. | y=$2\sqrt{{x^2}+2}+\frac{2}{{\sqrt{{x^2}+2}}}$ | ||
| C. | $y=sinx+\frac{4}{sinx}$(0<x<π) | D. | y=ex+4e-x |
1.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且$\frac{{S}_{1}}{{S}_{2}}$=$\frac{16}{9}$,则$\frac{{V}_{1}}{{V}_{2}}$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
2.已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{{m}^{2}}$=1(m>0)的焦距为8,则m的值为( )
| A. | 3或$\sqrt{41}$ | B. | 3 | C. | $\sqrt{41}$ | D. | ±3或$±\sqrt{41}$ |
19.若函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$图象的两条相邻的对称轴之间的距离为$\frac{π}{2}$,且该函数图象关于点(x0,0)成中心对称,${x_0}∈[0,\frac{π}{2}]$,则x0=( )
| A. | $\frac{π}{12}$ | B. | $\frac{5π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
20.设p:x<3,q:-1<x<2,则p是q成立的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
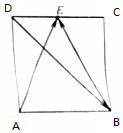
 已知扇环如图所示,∠AOB=120°,OA=2,OA′=$\frac{1}{2}$,P是扇环边界上一动点,且满足$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则2x+y的取值范围为[$\frac{1}{4}$,$\frac{2\sqrt{21}}{3}$].
已知扇环如图所示,∠AOB=120°,OA=2,OA′=$\frac{1}{2}$,P是扇环边界上一动点,且满足$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则2x+y的取值范围为[$\frac{1}{4}$,$\frac{2\sqrt{21}}{3}$].