题目内容
空间四边形ABCD中，点M，N分别是AB，CD的中点，且
=
，
=
，
=
，则用向量
，
，
表示向量
为 ．
| AB |
| b |
| AC |
| c |
| AD |
| d |
| b |
| c |
| d |
| MN |
考点：向量数乘的运算及其几何意义
专题：平面向量及应用
分析：据题意，画出图形，结合图形，求出向量
的大小．
| MN |
解答：
解：据题意，画出图形，如图所示；
∵点M，N分别是AB，CD的中点，
∴
=
=
，
=
（
+
）=
（
+
）；
∴
=
-
=
（
+
）-
=
+
-
．
故答案为：
+
-
．
解：据题意，画出图形，如图所示；∵点M，N分别是AB，CD的中点，
∴
| AM |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| b |
| AN |
| 1 |
| 2 |
| AD |
| AC |
| 1 |
| 2 |
| d |
| c |
∴
| MN |
| AN |
| AM |
| 1 |
| 2 |
| d |
| c |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| c |
| 1 |
| 2 |
| d |
| 1 |
| 2 |
| b |
故答案为：
| 1 |
| 2 |
| c |
| 1 |
| 2 |
| d |
| 1 |
| 2 |
| b |
点评：本题考查了平面向量的加法与减法的几何意义的应用问题，是基础题目．
练习册系列答案
相关题目
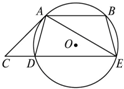如图，四边形ABED内接于⊙O，AB∥DE，AC切⊙O于A，交ED延长线于C．若AD=BE=