题目内容
已知f(x)=x2+2ax+2,x∈[-5,5]
(1)当a=-1时,求f(x)的最值;
(2)求f(x)的最小值;
(3)当f(x)在区间[-5,5]上为单调函数,求实数a的取值范围.
(1)当a=-1时,求f(x)的最值;
(2)求f(x)的最小值;
(3)当f(x)在区间[-5,5]上为单调函数,求实数a的取值范围.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)当a=-1时,由f(x)=x2-2x+2=(x-1)2+1,x∈[-5,5],利用二次函数的性质求得f(x)的最值.
(2)由于f(x)=(x+a)2+2-a2 的图象的对称轴方程为x=-a,x∈[-5,5],分类讨论求得f(x)的最小值.
(3)当f(x)在区间[-5,5]上为单调增函数时,则由-a≤-5,求得a的范围;当f(x)在区间[-5,5]上为单调减函数时,则由-a≥5,求得a的范围,再把这两个a的范围取并集,即得所求.
(2)由于f(x)=(x+a)2+2-a2 的图象的对称轴方程为x=-a,x∈[-5,5],分类讨论求得f(x)的最小值.
(3)当f(x)在区间[-5,5]上为单调增函数时,则由-a≤-5,求得a的范围;当f(x)在区间[-5,5]上为单调减函数时,则由-a≥5,求得a的范围,再把这两个a的范围取并集,即得所求.
解答:
解:(1)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,∵x∈[-5,5],
故当x=1时,f(x)取得最小值为1;当x=-5时,f(x)取得最大值为37.
(2)由于f(x)=x2+2ax+2=(x+a)2+2-a2 的图象的对称轴方程为x=-a,x∈[-5,5],
∴当-5≤-a≤5时,f(x)的最小值为2-a2;当-a<-5时,即a>5时,f(x)在[-5,5]上单调递增,f(x)的最小值为f(-5)=27-10a;
当-a>5时,即a<-5时,f(x)在[-5,5]上单调递减,f(x)的最小值为f(5)=27+10a.
故有f(x)min=
.
(3)当f(x)在区间[-5,5]上为单调增函数时,则由-a≤-5,求得a≥5;
当f(x)在区间[-5,5]上为单调减函数时,则由-a≥5,求得a≤-5,
故要求的a的范围是{a|a≥5,或a≤-5}.
故当x=1时,f(x)取得最小值为1;当x=-5时,f(x)取得最大值为37.
(2)由于f(x)=x2+2ax+2=(x+a)2+2-a2 的图象的对称轴方程为x=-a,x∈[-5,5],
∴当-5≤-a≤5时,f(x)的最小值为2-a2;当-a<-5时,即a>5时,f(x)在[-5,5]上单调递增,f(x)的最小值为f(-5)=27-10a;
当-a>5时,即a<-5时,f(x)在[-5,5]上单调递减,f(x)的最小值为f(5)=27+10a.
故有f(x)min=
|
(3)当f(x)在区间[-5,5]上为单调增函数时,则由-a≤-5,求得a≥5;
当f(x)在区间[-5,5]上为单调减函数时,则由-a≥5,求得a≤-5,
故要求的a的范围是{a|a≥5,或a≤-5}.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属基础题.

练习册系列答案
相关题目
运行如图所示的程序框图,则输出的所有实数对(x,y)所对应的点都在函数( )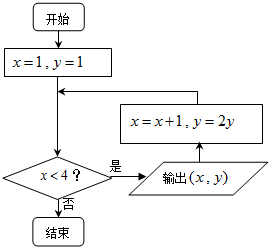

| A、f(x)=log2(x+1)的图象上 | ||
| B、f(x)=x2-2x+2的图象上 | ||
C、f(x)=
| ||
| D、f(x)=2x-1的图象上 |
下列命题正确的是( )
| A、垂直于同一直线的两条直线互相平行 |
| B、平行四边形在一个平面上的平行投影一定是平行四边形 |
| C、平面截正方体所得的截面图形可能是正六边形 |
| D、锐角三角形在一个平面上的平行投影不可能是钝角三角形 |
 某网店经营的一红消费品的进价为每件12元,周销售量p(件)与销售价格x(元)的关系,如图中折线所示,每周各项开支合计为20元.
某网店经营的一红消费品的进价为每件12元,周销售量p(件)与销售价格x(元)的关系,如图中折线所示,每周各项开支合计为20元.