题目内容

下列函数中既不是奇函数，又不是偶函数的是（　　）
A、y=x3
B、y=2|x|
C、y=|lgx|
D、y=tanx
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：分别根据函数奇偶性的定义和性质即可得到结论．
解答： 解：由函数奇偶性定义得y=x3，y=tanx是奇函数，y=2|x|是偶函数，
∵y=|lgx|的定义域为（0，+∞），
∴y=|lgx|既不是奇函数，又不是偶函数．
故选：C．
点评：本题主要考查函数奇偶性的判断，要求熟练掌握常见函数的奇偶性的特点，比较基础．
练习册系列答案
相关题目
i是虚数单位，复数z=
2i3
2+i
的虚部为
 
．
复数
2-i
1-i
（i为虚数单位）在复平面上对应的点所在的象限为（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
如图已知函数y=Asin（ωx+φ）的部分图象，则表达式为（　　）
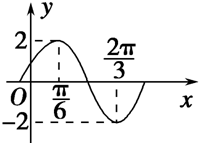
A、y=2sin(
10
11
x+
π
6
)
B、y=2sin(
10
11
x-
π
6
)
C、y=2sin(2x+
π
6
)
D、y=2sin(2x-
π
6
)
设a，b为正实数，现有下列命题：
①若a2-b2=1，则a-b＜1；
②若
1
b
-
1
a
=1，则a-b＜1；
③若|
a
-
b
|=1，则|a-b|＜1；
④若|a3-b3|=1，则|a-b|＜1．
其中真命题的个数有（　　）
A、1个B、2个C、3个D、4个
下列函数在定义域内为奇函数，且有最小值的是（　　）
A、y=x+
1
x
B、y=xsinx
C、y=x（|x|-1）
D、y=cos（x-
π
2
）
指出下列集合之间的关系
（1）集合A={x|x=2k+1，k∈Z}，集合B={x|x=4k±1，k∈Z}；
（2）集合A={x|x=2m，m∈Z}，集合B={x|x=4n±2，n∈Z}；
（3）集合A={x|x=
kπ
2
，k∈Z}，集合B={x|x=kπ或x=kπ+
π
2
，k∈Z}．
已知向量
a
=(1，-
3
)，
b
=（sinx，cosx），f（x）=
a
•
b
．
（Ⅰ）若f（θ）=0，求
2cos2
θ
2
-sinθ-1
2
sin(θ+
π
4
)
的值；
（Ⅱ）当x∈[0，π]时，求函数f（x）的值域．
设集合M={x|x2＜4} N={-1，1，2}，则M∩N=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网