题目内容
4.设复数z=3+4i,则复数z+$\frac{|z|}{z}$的虚部为( )| A. | $\frac{16}{5}$ | B. | $\frac{16}{5}$i | C. | $\frac{18}{5}$ | D. | $\frac{18}{5}$i |
分析 把z=3+4i代入复数z+$\frac{|z|}{z}$,然后利用复数代数形式的乘除运算化简得答案.
解答 解:∵z=3+4i,
∴$|z|=\sqrt{{3}^{2}+{4}^{2}}=5$,
∴z+$\frac{|z|}{z}$=$3+4i+\frac{5}{3+4i}=3+4i+\frac{5(3-4i)}{(3+4i)(3-4i)}$=$3+4i+\frac{3}{5}-\frac{4}{5}i=\frac{18}{5}+\frac{16}{5}i$,
∴复数z+$\frac{|z|}{z}$的虚部为$\frac{16}{5}$.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如表数据:
根据表中数据,得到$k=\frac{{50×{{(13×20-10×7)}^2}}}{23×27×20×30}≈4.844$,
参照独立性检验临界值表,则认为“选修文科与性别有关系”出错的可能性不超过0.05.
| 理科 | 文科 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
参照独立性检验临界值表,则认为“选修文科与性别有关系”出错的可能性不超过0.05.
15.已知$\frac{a+2i}{i}$=b+i(其中a,b∈R,i为虚数单位),则a+b的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
19.根据《环境空气质量指数(AQI)技术规定(试行)》(HJ633-2012)规定,空气污染指数划分为六档,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显,如表(1)所示,若表(2)、表(3)分别是石家庄市、北京市近期空气质量记录.
表一:
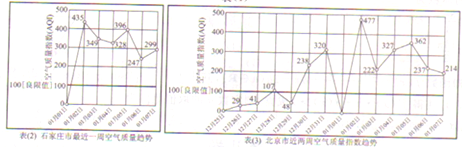
(Ⅰ)根据表(2)、表(3)中的数据,通过研究1月1日至7日石家庄市、北京市近一周空气污染指数的平均值,比较石家庄市、北京市近一周空气污染的严重程度(结果保留两位有效数字)
(Ⅱ)将1月1日至7日分别记为x,x=1,2,3,4,5,6,7,其对应的空气污染指数为y,根据表中提供的数据,用变量y与x的相关系数说明石家庄市空气污染指数y与日期x之间线性相关关系的强弱,丙说明理由
(Ⅲ)小明在北京经营一家洗车店,经小明统计,AQI指数不高于200时,洗车店平均每天亏损约200元,AQI指数在200至400时,洗车店平均每天收入约400元,AQI指数大于400时,洗车店平均每天收入约700元,求小明的洗车店在近两周每天收入的数学期望(结构保留整数部分)
附:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overrightarrow{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})}}$,r∈[0.30,0.75)时,相关性一般,r∈[0.75,1]时,相关性很强
参考数据:$\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}$=28,$\sum_{i=1}^{n}$(y1-$\overline{y}$)2≈123134,$\sum_{i=1}^{n}$(xi-$\overline{x}$)(y1-$\overline{y}$)=$\stackrel{•}{5}$68,$\sqrt{3447752}$≈1857.
表一:
| 空气质量指数 | [0,50] | [51,100] | [101,150] | [151,200] | [201,300] | 300以上 |
| 空气质量状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |

(Ⅰ)根据表(2)、表(3)中的数据,通过研究1月1日至7日石家庄市、北京市近一周空气污染指数的平均值,比较石家庄市、北京市近一周空气污染的严重程度(结果保留两位有效数字)
(Ⅱ)将1月1日至7日分别记为x,x=1,2,3,4,5,6,7,其对应的空气污染指数为y,根据表中提供的数据,用变量y与x的相关系数说明石家庄市空气污染指数y与日期x之间线性相关关系的强弱,丙说明理由
(Ⅲ)小明在北京经营一家洗车店,经小明统计,AQI指数不高于200时,洗车店平均每天亏损约200元,AQI指数在200至400时,洗车店平均每天收入约400元,AQI指数大于400时,洗车店平均每天收入约700元,求小明的洗车店在近两周每天收入的数学期望(结构保留整数部分)
附:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overrightarrow{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})}}$,r∈[0.30,0.75)时,相关性一般,r∈[0.75,1]时,相关性很强
参考数据:$\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}$=28,$\sum_{i=1}^{n}$(y1-$\overline{y}$)2≈123134,$\sum_{i=1}^{n}$(xi-$\overline{x}$)(y1-$\overline{y}$)=$\stackrel{•}{5}$68,$\sqrt{3447752}$≈1857.
13.设i是叙述虚数单位,若复数2-$\frac{a}{2-i}$(a∈R)是纯虚数,则a的值为( )
| A. | 5 | B. | 3 | C. | -5 | D. | -3 |
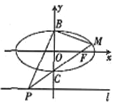 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2