题目内容
已知椭圆的中心在坐标原点,左焦点为F(-
,0),右顶点为D(2,0),设点A(2,2).
(Ⅰ)求这个椭圆的标准方程;
(Ⅱ)P是椭圆上的动点,求线段PA中点M的轨迹方程;
(Ⅲ)过点(-1,0)的直线L交椭圆于点B,C,求△ABC面积等于4的直线L的方程.
| 3 |
(Ⅰ)求这个椭圆的标准方程;
(Ⅱ)P是椭圆上的动点,求线段PA中点M的轨迹方程;
(Ⅲ)过点(-1,0)的直线L交椭圆于点B,C,求△ABC面积等于4的直线L的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知得椭圆的半长轴a=2,半焦距c=
,则半短轴b=1.又椭圆的焦点在x轴上,由此能求出椭圆的标准方程.
(Ⅱ)由点A(2,2),设P(2cosθ,sinθ),线段PA中点M(x,y),且
,由此能求出线段PA中点M的轨迹方程.
(Ⅲ)设过点(-1,0)的直线L的方程为y=k(x+1),联立
,得(4k2+1)x2+8k2x+4k2-4=0,由此利用弦长公式和点到直线的距离公式能求出直线的方程.
| 3 |
(Ⅱ)由点A(2,2),设P(2cosθ,sinθ),线段PA中点M(x,y),且
|
(Ⅲ)设过点(-1,0)的直线L的方程为y=k(x+1),联立
|
解答:
解:(Ⅰ)由已知得椭圆的半长轴a=2,
半焦距c=
,则半短轴b=1.
又椭圆的焦点在x轴上,
∴椭圆的标准方程为
+y2=1.
(Ⅱ)∵点A(2,2),P是椭圆
+y2=1上的动点,
∴设P(2cosθ,sinθ),
∴线段PA中点M(x,y),且
,
∴线段PA中点M的轨迹方程为:(x-1)2+4(y-1)2=1.
(Ⅲ)设过点(-1,0)的直线L的方程为y=k(x+1),
联立
,得(4k2+1)x2+8k2x+4k2-4=0,
设B(x1,y1),C(x2,y2),则x1+x2=
,x1x2=
,
|BC|=
,
点A(2,2)到直线y=k(x+1)的距离d=
,
∵△ABC面积等于4,
∴S△ABC=
d|BC|=
×
×
=4,
解得k=0,
∴直线L的方程为y=0.
半焦距c=
| 3 |
又椭圆的焦点在x轴上,
∴椭圆的标准方程为
| x2 |
| 4 |
(Ⅱ)∵点A(2,2),P是椭圆
| x2 |
| 4 |
∴设P(2cosθ,sinθ),
∴线段PA中点M(x,y),且
|
∴线段PA中点M的轨迹方程为:(x-1)2+4(y-1)2=1.
(Ⅲ)设过点(-1,0)的直线L的方程为y=k(x+1),
联立
|
设B(x1,y1),C(x2,y2),则x1+x2=
| -8k2 |
| 4k2+1 |
| 4k2-4 |
| 4k2+1 |
|BC|=
(1+k2)[(
|
点A(2,2)到直线y=k(x+1)的距离d=
| |k-2| | ||
|
∵△ABC面积等于4,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| |k-2| | ||
|
(1+k2)[(
|
解得k=0,
∴直线L的方程为y=0.
点评:本题考查椭圆的标准方程、线段PA中点M的轨迹方程和直线L的方程的求法,解题时要认真审题,注意弦长公式和点到直线的距离公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知m,n是不重合的两条直线,α,β是不重合的两个平面.下列命题:
①若α⊥β,m⊥α,则m∥β;
②若m⊥α,m⊥β,则α∥β;
③若m∥α,m⊥n,则n⊥α;
④若m∥α,m?β,则α∥β.
其中所有真命题的序号是( )
①若α⊥β,m⊥α,则m∥β;
②若m⊥α,m⊥β,则α∥β;
③若m∥α,m⊥n,则n⊥α;
④若m∥α,m?β,则α∥β.
其中所有真命题的序号是( )
| A、② | B、④ | C、②④ | D、①② |
边长为a的正方形ABCD沿对角线BD折成90°的二面角,则AC的长为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、a |
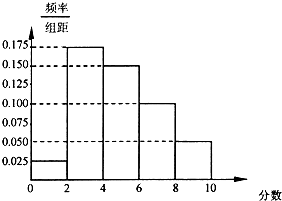 某个团购网站为了更好地满足消费者,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是10分.上个月该网站共卖出了100份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.
某个团购网站为了更好地满足消费者,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是10分.上个月该网站共卖出了100份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.