题目内容
6.如图所示的几何体中,ABC-A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.(Ⅰ)若AA1=AC,求证:AC1⊥平面A1B1CD;

(Ⅱ)若CD=2,AA1=λAC,二面角C-A1D-C1的余弦值为$\frac{\sqrt{2}}{4}$,求三棱锥C1-A1CD的体积.
分析 (Ⅰ)若AA1=AC,根据线面垂直的判定定理即可证明AC1⊥平面A1B1CD;
(Ⅱ)建立坐标系,根据二面角C-A1D-C1的余弦值为$\frac{\sqrt{2}}{4}$,求出λ的值,根据三棱锥的体积公式进行计算即可.
解答 证明:(Ⅰ)若AA1=AC,则四边形ACC1A1为正方形,则AC1⊥A1C,
∵AD=2CD,∠ADC=60°,∴△ACD为直角三角形,则AC⊥CD,
∵AA1⊥平面ABC,∴CD⊥平面ACC1A1,则CD⊥A1C,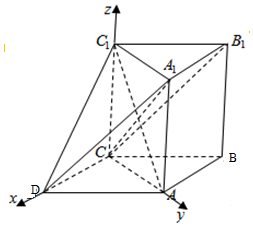
∵A1C∩CD=C,∴AC1⊥平面A1B1CD;
(Ⅱ)若CD=2,∵∠ADC=60°,∴AC=2$\sqrt{3}$,
则AA1=λAC=2$\sqrt{3}$λ,建立以C为坐标原点,CD,CB,CC1分别为x,y,z轴的空间直角坐标系如图:
则C(0,0,0),D(2,0,0),A(0,2$\sqrt{3}$,0),C1(0,0,2$\sqrt{3}$λ),A1(0,2$\sqrt{3}$,2$\sqrt{3}$λ),
则$\overrightarrow{{A}_{1}D}$=(2,-2$\sqrt{3}$,-2$\sqrt{3}$λ),$\overrightarrow{CD}$=(2,0,0),$\overrightarrow{{C}_{1}{A}_{1}}$=(0,2$\sqrt{3}$,0),
设面CA1D的一个法向量为$\overrightarrow{m}$=(1,0,0).
则$\overrightarrow{m}$•$\overrightarrow{{A}_{1}D}$=2x-2$\sqrt{3}$y-2$\sqrt{3}$λz=0,$\overrightarrow{m}$•$\overrightarrow{CD}$=2x=0,
则x=0,y=-λz,令z=1,则y=-λ,则$\overrightarrow{m}$=(0,-λ,1)
设面A1DC1的一个法向量为$\overrightarrow{n}$=(x,y,z)
$\overrightarrow{n}$•$\overrightarrow{{A}_{1}D}$=2x-2$\sqrt{3}$y-2$\sqrt{3}$λz=0,$\overrightarrow{n}$•$\overrightarrow{{C}_{1}{A}_{1}}$=2$\sqrt{3}$y=0,
则y=0,2x-2$\sqrt{3}$λz=0,令z=1,则x=$\sqrt{3}$λ,
则$\overrightarrow{n}$=($\sqrt{3}$λ,0,1),
∵二面角C-A1D-C1的余弦值为$\frac{\sqrt{2}}{4}$,
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{1+{λ}^{2}•\sqrt{1+3{λ}^{2}}}}$=$\frac{\sqrt{2}}{4}$,
即(1+λ2)(1+3λ2)=8,
得λ=1,
即AA1=AC,
则三棱锥C1-A1CD的体积V=V${\;}_{D-{A}_{1}{C}_{1}C}$=$\frac{1}{3}CD•\frac{1}{2}AC•A{A}_{1}$=$\frac{1}{3}×2×\frac{1}{2}×2\sqrt{3}×2\sqrt{3}$=4.
点评 本题主要考查线面垂直的判断以及三棱锥体积的计算,根据二面角的关系建立坐标系求出λ的值是解决本题的关键.

| A. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| B. | “a=3”是“函数f(x)=logax在定义域上为增函数”的充分不必要条件 | |
| C. | 若命题p:?n∈N,3n>100,则¬p:?n∈N,3n≤100 | |
| D. | 命题“?x∈(-∞,0),3x<5x”是真命题 |
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
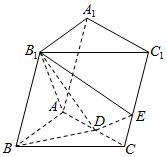 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.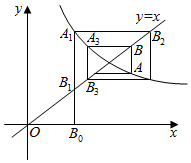 如图所示,折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴,A1,A2,…,An…这些点在函数y=$\frac{2}{x-1}$(x>1)图象上,B1,B2…Bn…这些点在直线y=x上,设点An的纵坐标为yn.
如图所示,折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴,A1,A2,…,An…这些点在函数y=$\frac{2}{x-1}$(x>1)图象上,B1,B2…Bn…这些点在直线y=x上,设点An的纵坐标为yn.