题目内容
16．已知△ABC的内角A、B、C所对的边的长分别是a、b、c．若a2+ab+b2-c2=0，则角C的大小是（ ）| A． | 30° | B． | 60° | C． | 120° | D． | 150° |
分析 利用余弦定理表示出cosC，将已知等式变形后代入求出cosC的值，由C为三角形的内角，利用特殊角的三角函数值即可求出C的度数．
解答 解：△ABC中，∵a2+ab+b2-c2=0，即a2+b2-c2=-ab，
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{-ab}{2ab}$=-$\frac{1}{2}$，
∵C为三角形的内角，
∴C=120°．
故选：C．
点评 此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键，属于基础题．
练习册系列答案
相关题目
7．已知i为虚数单位，复数z1=1+i，z2=1-i，则$\frac{z_1}{z_2}$=（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -i | D． | i |
11．某产品的广告费用x与销售额y的统计数据如表：
根据上表可得回归方程y=bx+a的b为9.2，据此模型预报广告费用为6万元时销售额为（ ）
| 广告费用x（万元） | 4 | 2 | 3 | 5 |
| 销售额y（万元） | 49 | 26 | 39 | 54 |
| A． | 63.6万 | B． | 65万 | C． | 66.1万 | D． | 67.7万 |
8．已知椭圆C：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点分别为F1，F2，M为C上位于第一象限的点，|MF1|=2，且MF1⊥y轴，MF2与椭圆C交于另一点N，若$\overrightarrow{M{F}_{2}}$=2$\overrightarrow{{F}_{2}N}$，则直线MN的斜率为（ ）
| A． | -$\frac{\sqrt{5}}{2}$ | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{5}$ |
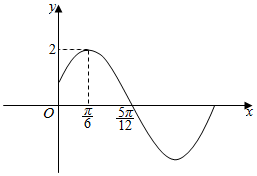已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．