题目内容
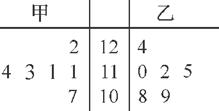
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:g)是否合格,分别记录抽查数据,获得重量数据茎叶图,如图所示.
(1) 根据样本数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对稳定;
(2) 若从乙车间6件样品中随机抽取两件,求所抽取两件样品重量之差不超过2 g的概率.
(1) 设甲、乙两个车间产品重量的均值分别为 ,
,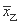 ,方差分别为
,方差分别为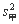 ,
,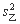 ,
,
则 =
=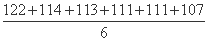 =113,
=113,
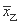 =
=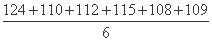 =113.
=113.
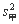 =
=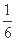 ×[(122-113)2+(114-113)2+(113-113)2+(111-113)2+(111-113)2+(107-113)2]=21,
×[(122-113)2+(114-113)2+(113-113)2+(111-113)2+(111-113)2+(107-113)2]=21,
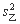 =
=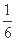 ×[(124-113)2+(110-113)2+(112-113)2+(115-113)2+(108-113)2+(109-113)2]≈29.33,
×[(124-113)2+(110-113)2+(112-113)2+(115-113)2+(108-113)2+(109-113)2]≈29.33,
因为 =
=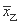 ,
,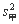 <
<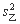 ,所以甲车间的产品的重量相对稳定.
,所以甲车间的产品的重量相对稳定.
(2) 从乙车间6件样品中随机抽取两件,结果共有15种:(124,110),(124,112),(124,115),(124,108),(124,109),(110,112),(110,115),(110,108),(110,109),(112,115),(112,108),(112,109),(115,108),(115,109),(108,109).
设所抽取两件样品重量之差不超过2g的事件为A,则事件A共有4个结果:(110,112),(110,108),(110,109),(108,109).
所以P(A)=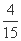 .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
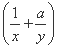 ≥9对任意正实数x,y恒成立,那么正实数a的最小值为 .
≥9对任意正实数x,y恒成立,那么正实数a的最小值为 .  若f(6-a2)>f(5a),则实数a的取值范围是 .
若f(6-a2)>f(5a),则实数a的取值范围是 . 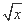 )8的展开式中不含x4项的系数的和为 .
)8的展开式中不含x4项的系数的和为 . A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.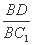 的值.
的值.