题目内容
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1) 求d,an;
(2) 若d<0,求|a1|+|a2|+|a3|+…+|an|.
(1) 由已知得
(2a2+2)2=5a1a34(a1+d+1)2=5a1(a1+2d)(11+d)2=25(5+d) 121+22d+d2=125+25dd2-3d-4=0d=4或d=-1.当d=4时,an=4n+6;当d=-1时,an=11-n.
(2) 由(1)知,当d<0时,an=11-n.
①当1≤n≤11时,
an≥0,所以|a1|+|a2|+|a3|+…+|an|=a1+a2+a3+…+an=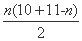 =
=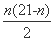 ;
;
②当12≤n时,
an<0,所以|a1|+|a2|+|a3|+…+|an|=a1+a2+a3+…+a11-(a12+a13+…+an)=2(a1+a2+a3+…+a11)-(a1+a2+a3+…+an)=2×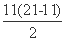 -
-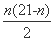 =
=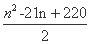 .
.
所以,综上所述,|a1|+|a2|+|a3|+…+|an|=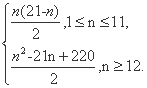

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
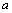 、b、c均为实数,且
、b、c均为实数,且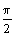 ,b=y2-2z+
,b=y2-2z+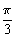 ,c=z2-2x+
,c=z2-2x+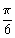 ,求证:
,求证: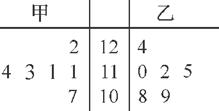
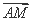 =λ
=λ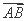 +μ
+μ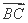 ,则λ+μ= .
,则λ+μ= . 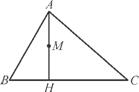
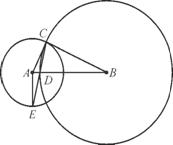
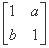 对应的变换将点A(1,1)变为A'(0,2),将曲线C:xy=1变为曲线C',求:
对应的变换将点A(1,1)变为A'(0,2),将曲线C:xy=1变为曲线C',求: