题目内容
三棱锥P-ABC,PA⊥平面ABC,PA=AB=AC,∠BAC=90°,E为PC中点,则PA与BE所成角的余弦值为 .
考点:异面直线及其所成的角
专题:空间角
分析:画出图形,找出PA与BE所成角的平面角,然后求出余弦值即可.
解答:
 解:三棱锥P-ABC,PA⊥平面ABC,PA=AB=AC,∠BAC=90°,E为PC中点,如图:过E作ED∥PA,交AC于D,DE⊥平面ABC,连结BD,则∠DEB为PA与BE所成角,
解:三棱锥P-ABC,PA⊥平面ABC,PA=AB=AC,∠BAC=90°,E为PC中点,如图:过E作ED∥PA,交AC于D,DE⊥平面ABC,连结BD,则∠DEB为PA与BE所成角,
设:PA=AB=AC=2,则DE=1,DB2=AD2+AB2,解得DE=
,
BE=
=
,
∴cos∠DEB=
=
=
.
故答案为:
.
 解:三棱锥P-ABC,PA⊥平面ABC,PA=AB=AC,∠BAC=90°,E为PC中点,如图:过E作ED∥PA,交AC于D,DE⊥平面ABC,连结BD,则∠DEB为PA与BE所成角,
解:三棱锥P-ABC,PA⊥平面ABC,PA=AB=AC,∠BAC=90°,E为PC中点,如图:过E作ED∥PA,交AC于D,DE⊥平面ABC,连结BD,则∠DEB为PA与BE所成角,设:PA=AB=AC=2,则DE=1,DB2=AD2+AB2,解得DE=
| 5 |
BE=
(
|
| 6 |
∴cos∠DEB=
| DE |
| BE |
| 1 | ||
|
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本题考查异面直线所成角的求法,作出异面直线所成角是解题的关键.

练习册系列答案
相关题目
如图是某几何体的三视图,则该几何体的体积等于( )
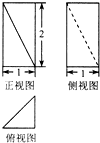

A、
| ||
B、
| ||
| C、1 | ||
D、
|
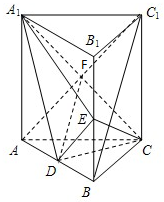 如图,直三棱柱ABC-A1B1C1中,D、E分别为AB、BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D、E分别为AB、BB1的中点.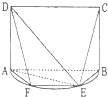 如图,E是以AB为直径的半圆O上异于点A,B的点,边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面.
如图,E是以AB为直径的半圆O上异于点A,B的点,边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面.