题目内容
17.根据条件求解下列问题(1)函数f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(-1<x<2)}\\{2x(x≥2)}\end{array}\right.$,若f(x)=3,求x;
(2)求函数的值域:y=$\frac{3x-1}{x+1}$.
分析 (1)由各段的函数值等于3求解得答案;
(2)把已知函数解析式变形,利用反比例型函数的值域求解.
解答 解:(1)由f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(-1<x<2)}\\{2x(x≥2)}\end{array}\right.$,且f(x)=3,得
$\left\{\begin{array}{l}{x+2=3}\\{x≤-1}\end{array}\right.$①,或$\left\{\begin{array}{l}{{x}^{2}=3}\\{-1<x<2}\end{array}\right.$②,或$\left\{\begin{array}{l}{2x=3}\\{x≥2}\end{array}\right.$.
解得①得:x不存在,解②得:x=$\sqrt{3}$,解③得:x不存在.
∴x=$\sqrt{3}$;
(2)y=$\frac{3x-1}{x+1}$=$\frac{3(x+1)-4}{x+1}=3-\frac{4}{x+1}$.
∵$\frac{4}{x+1}≠0$,∴3-$\frac{4}{x+1}≠3$.
故函数y=$\frac{3x-1}{x+1}$的值域为{y|y≠3}.
点评 本题考查函数的零点与方程根的关系,考查了函数值域的求法,体现了分类讨论的数学思想方法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知三棱锥P-A BC四个顶点都在半径为2的球面上,PA⊥面ABC,PA=2,底面ABC是正三角形,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )
| A. | $\frac{7π}{4}$ | B. | 2π | C. | $\frac{9π}{4}$ | D. | 3π |
2.已知等差数列{an}中,a3+a11=50,a4=13,则数列{an}的公差等于( )
| A. | 1 | B. | 4 | C. | 5 | D. | 6 |
6.笼内关有6只果蝇,不慎混入2只苍蝇,只好把笼子打开一个小孔,让蝇子一只一只飞出去,直到2只苍蝇都飞出笼子时,笼内还有3只果蝇的概率等于( )
| A. | $\frac{27}{256}$ | B. | $\frac{1}{7}$ | C. | $\frac{5}{14}$ | D. | $\frac{27}{64}$ |
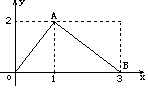 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),
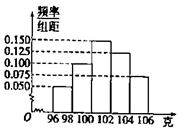 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),(104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),(104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )