题目内容
3.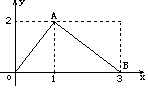 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•(x-1),则函数g(x)最大值为1.
分析 先根据函数f(x)的图象求出解析式,再根据g(x)=f(x)•(x-1)求得函数g(x)的解析式,分段求出最大值,则函数g(x)最大值可求.
解答 解:如图,由图可知,
函数f(x)的解析式为:f(x)=$\left\{\begin{array}{l}{2x,0≤x≤1}\\{-x+3,1<x≤3}\end{array}\right.$,
又∵g(x)=f(x)•(x-1),
∴函数g(x)的解析式为:
g(x)=$\left\{\begin{array}{l}{2{x}^{2}-2x,0≤x≤1}\\{-{x}^{2}+4x-3,1<x≤3}\end{array}\right.$,
当0≤x≤1时,g(x)=$2(x-\frac{1}{2})^{2}-\frac{1}{2}$,
∴g(x)max=g(1)=g(0)=0;
当1<x≤3时,g(x)=-(x-2)2+1≤1.
∴函数g(x)最大值为1,
故答案为:1.
点评 本题考查的是分段函数解析式的求法和分段函数求最值的求法,体现了数形结合、分类讨论及数学转化思想方法,是中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
18.将数字“123367”重新排列后得到不同的偶数个数为( )
| A. | 72 | B. | 120 | C. | 192 | D. | 240 |
8.数列0,1,0,1,0,1,0,1,…的一个通项公式是( )
| A. | $\frac{{{{(-1)}^n}+1}}{2}$ | B. | $cos\frac{nπ}{2}$ | C. | $cos\frac{(n+1)π}{2}$ | D. | $cos\frac{(n+2)π}{2}$ |
12.在极坐标系中,直线$ρcos(θ-\frac{π}{4})=\sqrt{2}$与曲线$ρ=\sqrt{2}$的公共点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 以上都有可能 |