Question

5．已知三棱锥P-A BC四个顶点都在半径为2的球面上，PA⊥面ABC，PA=2，底面ABC是正三角形，点E是线段AB的中点，过点E作球O的截面，则截面面积的最小值是（　　）

• A． $\frac{7π}{4}$
• B． 2π
• C． $\frac{9π}{4}$
• D． 3π

Answer 1

分析 设正△ABC的中心为O₁，连结O₁A．根据球的截面圆性质、正三角形的性质与勾股定理，而经过点E的球O的截面，当截面与OE垂直时截面圆的半径最小，相应地截面圆的面积有最小值，由此算出截面圆半径的最小值，从而可得截面面积的最小值．

解答 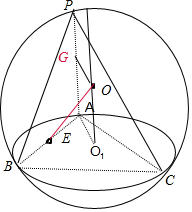解：设正△ABC的中心为O₁，连结O₁A，∵O₁是正△ABC的中心，A、B、C三点都在球面上，
∴O₁O⊥平面ABC，∵PA⊥面ABC，PA=2，∴球心O到平面ABC的距离为O₁O=$\frac{1}{2}PA$=1，
∴Rt△O₁OA中，O₁A=$\sqrt{O{A}^{2}-O{{O}_{1}}^{2}}=\sqrt{3}$，∴又∵E为AB的中点，△ABC是等边三角形，∴AE=AO₁cos30°=$\frac{3}{2}$．
∵过E作球O的截面，当截面与OE垂直时，截面圆的半径最小，
∴当截面与OE垂直时，截面圆的面积有最小值．
此时截面圆的半径r=$\frac{3}{2}$，可得截面面积为S=πr²=$\frac{9π}{4}$，
故选：C．

点评 本题已知球的内接正三角形与球心的距离，求经过正三角形中点的最小截面圆的面积．着重考查了勾股定理、球的截面圆性质与正三角形的性质等知识，属于中档题．