题目内容
14.已知两个不等的锐角α、β满足xsinβ+ycosα=sinα,xsinα+ycosβ=sinβ,其中α+β≠$\frac{π}{2}$,且x,y∈R.则x2-y2的值是1.分析 根据条件求出x,y的值,然后进行化简求解即可.
解答 解:由xsinβ+ycosα=sinα,xsinα+ycosβ=sinβ,得x=$\frac{sinβcosα-sinαcosβ}{sinαcosα-sinβcosβ}$=$\frac{2sin(β-α)}{sin2α-sin2β}$=$\frac{2sin(β-α)}{2cos(α+β)sin(α-β)}$=-$\frac{1}{cos(α+β)}$=-sec(α+β),
y=$\frac{sin^2-sin^2β}{sinαcosα-sinβcosβ}$=$\frac{cos2β-cos2α}{sin2α-sin2β}$=$\frac{sin(α+β)sin(α-β)}{sin(α-β)cos(α+β)}$=tan(α+β),
则x2-y2=[-sec(α+β)]2-tan2(α+β)=1,
故答案为:1.
点评 本题主要考查三角函数值的化简和求解,根据条件求出x,y的值是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
5.在等差数列中,连续四项为a,x,b,2x,那么a:b=( )
| A. | 1:4 | B. | 1:3 | C. | 1:3或1 | D. | 1:2 |
2.复数z满足$\frac{z}{z-i}$=i(i为虚数单位),则$\overline{z}$=( )
| A. | 1+i | B. | 1-i | C. | $\frac{1+i}{2}$ | D. | $\frac{1-i}{2}$ |
19.在平面直角坐标系xOy中,设锐角α的终边与圆O:x2+y2=1交于点M(x1,y1),点M沿圆O逆时针移动$\frac{π}{3}$个单位弧长后到达点N,设点N的坐标为(x2,y2),则x1•x2的取值范围是( )
| A. | (0,$\frac{\sqrt{3}}{2}$) | B. | (-$\frac{1}{4}$,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,1] | D. | [-$\frac{1}{4}$,$\frac{1}{2}$) |
3.向量$\overrightarrow{m}$=(8,-4)在向量$\overrightarrow{n}$=(2,1)上的投影为( )
| A. | $\frac{6}{5}$ | B. | $\frac{12}{5}$ | C. | $\frac{6\sqrt{5}}{5}$ | D. | $\frac{12\sqrt{5}}{5}$ |
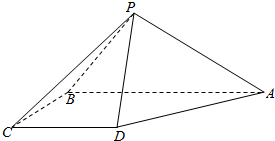 如图,四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD为直角梯形,AB=2CD=2BC=2,AB∥CD,AB⊥BC,△PAB为等腰直角三角形且PA⊥PB.
如图,四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD为直角梯形,AB=2CD=2BC=2,AB∥CD,AB⊥BC,△PAB为等腰直角三角形且PA⊥PB.