Question

4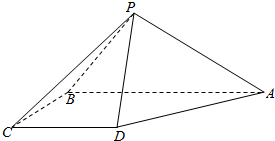．如图，四棱锥P-ABCD中，平面PAB⊥平面ABCD，底面ABCD为直角梯形，AB=2CD=2BC=2，AB∥CD，AB⊥BC，△PAB为等腰直角三角形且PA⊥PB．
（1）求证：平面PBC⊥平面PAB．
（2）在线段PA上求一点E，使PC∥平面EBD，并求出$\frac{PE}{PA}$的值．
（3）在（2）的条件下求三棱锥P-EBD的体积．

Answer 1

分析 （1）根据平面PAB⊥平面ABCD可得BC⊥平面PAB，故平面PBC⊥平面PAB；
（2）连结AC，BD，交点为O，则△OCD∽△OAB，于是$\frac{OC}{OA}=\frac{CD}{AB}=\frac{1}{2}$，故而$\frac{PE}{PA}=\frac{CO}{CA}=\frac{1}{3}$．
（3）用棱锥P-ABD的体积减去棱锥E-ABD的体积即可．

解答 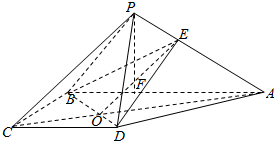证明：（1）∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，BC⊥AB，BC?平面ABCD，
∴BC⊥平面PAB，∵BC?平面PBC，
∴平面PBC⊥平面PAB．
（2）连结AC，BD，交点为O，则△OCD∽△OAB，
∴$\frac{OC}{OA}=\frac{CD}{AB}=\frac{1}{2}$．∴$\frac{CO}{CA}=\frac{1}{3}$．
∵PC∥平面EBD，PC?平面PAC，平面PAC∩平面EBD=OE，
∴PC∥OE．
∴$\frac{PE}{PA}=\frac{CO}{CA}$=$\frac{1}{3}$．
（3）取AB中点F，连结PF，则PF⊥AB，
∴PF⊥平面ABCD，PF=$\frac{1}{2}AB=1$．
∴点E到平面ABCD的距离d=$\frac{2}{3}PF=\frac{2}{3}$．
∴三棱锥P-EBD的体积V=V_棱锥P-ABD-V_棱锥E-ABD=$\frac{1}{3}{V}_{棱锥P-ABD}$=$\frac{1}{3}×\frac{1}{3}×\frac{1}{2}×AB×BC×PF$=$\frac{1}{9}$．

点评 本题考查了面面垂直的判断，线面平行的性质，棱锥的体积计算，属于中档题．