题目内容
10.已知定义在R上的奇函数f(x)满足f(x+2)=f(x),且在(0,1]上,满足f(x)=$\frac{x^2-x}{2}$,则f(-2016)+f(-2016$\frac{1}{2}$)=( )| A. | 0 | B. | $\frac{1}{4}$ | C. | -$\frac{1}{8}$ | D. | $\frac{1}{8}$ |
分析 根据函数奇偶性和周期性的性质进行求解即可.
解答 解:f(-2016)=f(-2014)=f(-2012)=…=f(0)=0,
$f({-2016\frac{1}{2}})=f({-2014\frac{1}{2}})=f({-2012\frac{1}{2}})=…=f({-\frac{1}{2}})=-f({\frac{1}{2}})=-\frac{{{{({\frac{1}{2}})}^2}-({\frac{1}{2}})}}{2}=\frac{1}{8}$,
所以$f({-2016})+f({-2016\frac{1}{2}})=0+\frac{1}{8}=\frac{1}{8}$.
故选:D.
点评 本题主要考查函数值的计算,根据函数奇偶性和周期性的关系进行转化是解决本题的关键.

练习册系列答案
相关题目
1.在△ABC中,已知a=2,A=45°,B=120°,则b=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
18.已知等差数列{an}的前n项和为Sn,若a3+a4=5,则S6=( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
2.方程y=k(x-1)表示( )
| A. | 过点(-1,0)的所有直线 | B. | 过点(1,0)的所有直线 | ||
| C. | 过点(1,0)且不垂直于x轴的所有直线 | D. | 过点(1,0)且除去x轴的所有直线 |
19.已知集合A={1,4,x},B={1,x2},且B⊆A,则满足条件的实数x有( )
| A. | 1 个 | B. | 2 个 | C. | 3个 | D. | 4个 |
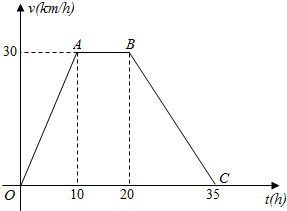 据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).