题目内容
求下列函数的驻点、极值点和对应的极值,有条件时用计算机或计算器作图对照.
(1)f(x)=2x2-6x+1;
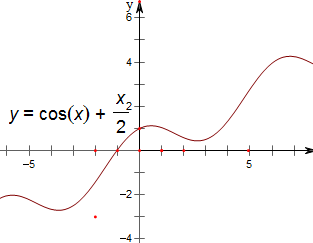
(2)g(x)=cosx+
;
(3)f(x)=2x3+3x2+6x-7;
(4)h(x)=x2ex.
(1)f(x)=2x2-6x+1;
(2)g(x)=cosx+
| x |
| 2 |
(3)f(x)=2x3+3x2+6x-7;
(4)h(x)=x2ex.
考点:利用导数研究函数的极值,导数的运算
专题:计算题,作图题,导数的综合应用
分析:对四个函数依次求导并令导数为0,从而解出函数的驻点,再检验驻点附近导数的正负,从而确定是不是极值点,再求极值.
解答:
解:(1)∵f(x)=2x2-6x+1,
∴令f′(x)=4x-6=0解得,
x=
,
故x=
为函数的驻点,
又∵在x=
附近,左侧f′(x)<0,右侧f′(x)>0;
∴x=
是函数的极小值点,极小值为f(
)=-
;
如下图,

(2)∵g(x)=cosx+
,
∴令g′(x)=-sinx+
=0,
故x=2kπ+
和x=2kπ+
,(k∈Z)是函数的驻点,
且判断x=2kπ+
和x=2kπ+
(k∈Z)是函数的也是函数的极值点,
当x=2kπ+
时有极大值g(2kπ+
)=
+kπ+
,(k∈Z);
当x=2kπ+
时有极小值g(2kπ+
)=-
+kπ+
,(k∈Z);
如下图,
(3)f′(x)=6x2+6x+6=6[(x+
)2+
]>0,
故函数没有驻点,极值点;
如下图,

(4)令h′(x)=x2ex+2xex=(2x+x2)ex=0解得,
x=0或x=-2;
故x=0和x=-2是函数的驻点,
且易知x=0和x=-2分别是函数的极小值点与极大值点;
极小值h(0)=0,极大值h(-2)=
.
如下图,

∴令f′(x)=4x-6=0解得,
x=
| 3 |
| 2 |
故x=
| 3 |
| 2 |
又∵在x=
| 3 |
| 2 |
∴x=
| 3 |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
如下图,

(2)∵g(x)=cosx+
| x |
| 2 |
∴令g′(x)=-sinx+
| 1 |
| 2 |
故x=2kπ+
| π |
| 6 |
| 5π |
| 6 |
且判断x=2kπ+
| π |
| 6 |
| 5π |
| 6 |
当x=2kπ+
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| π |
| 12 |
当x=2kπ+
| 5π |
| 6 |
| 5π |
| 6 |
| ||
| 2 |
| 5π |
| 12 |
如下图,

(3)f′(x)=6x2+6x+6=6[(x+
| 1 |
| 2 |
| 3 |
| 4 |
故函数没有驻点,极值点;
如下图,

(4)令h′(x)=x2ex+2xex=(2x+x2)ex=0解得,
x=0或x=-2;
故x=0和x=-2是函数的驻点,
且易知x=0和x=-2分别是函数的极小值点与极大值点;
极小值h(0)=0,极大值h(-2)=
| 4 |
| e2 |
如下图,

点评:本题考查了导数的综合应用及学生作图的能力,属于难题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,已知点A(-2,0)和圆O:x2+y2=4,AB是圆O的直经,从左到右M、O和N依次是AB的四等分点,P(异于A、B)是圆O上的动点,PD⊥AB交AB于D,
如图,已知点A(-2,0)和圆O:x2+y2=4,AB是圆O的直经,从左到右M、O和N依次是AB的四等分点,P(异于A、B)是圆O上的动点,PD⊥AB交AB于D,