设全集U=R.集合A={x|x(x-3)＞0}.则∁UA=( )A．[0.3]B．(0.3)C．D．题目和参考答案——青夏教育精英家教网——

题目内容

10．设全集U=R，集合A={x|x（x-3）＞0}，则∁_UA=（　　）

A．

[0，3]

B．

（0，3）

C．

（-∞，0）∪（3，+∞）

D．

（-∞，0]∪[3，+∞）

分析化简集合A，求出A在全集中的补集∁_UA即可．

解答解：因为A={x|x（x-3）＞0}={x|x＜0或x＞3}，
所以∁_UA={x|0≤x≤3}=[0，3]．
故选：A．

点评本题考查了集合的化简与运算问题，是基础题目．

练习册系列答案

第1考场期末大考卷系列答案

暑假作业西安出版社系列答案

新课堂同步阅读系列答案

优佳学案云南省初中学业水平考试总复习系列答案

暑假篇假期园地广西师范大学出版社系列答案

南方新课堂快乐暑假系列答案

百年学典快乐假期暑假作业系列答案

暑假提优40天系列答案

黄冈状元成才路状元作业本系列答案

1加1好成绩暑假作业沈阳出版社系列答案

相关题目

4．在三角形ABC中，若$\overrightarrow{AB}•\overrightarrow{BC}$＞0，则三角形ABC的形状为钝角三角形．

1．将$y=cos（{2x+\frac{π}{4}}）$的图象向右平移$\frac{π}{4}$个单位，则平移后图象的一个对称中心是（　　）

$（{\frac{3π}{8}，0}）$

$（{\frac{π}{8}，0}）$

$（{\frac{3π}{4}，0}）$

$（{\frac{π}{4}，0}）$

18．定义在R上的函数f（x）是偶函数，且f（x）=f（2-x）．若f（x）在区间[1，2]上是减函数，则$f（-\frac{π}{3}）\;，\;\;f（-\frac{3}{2}）$的大小关系为$f（-\frac{π}{3}）＞f（-\frac{3}{2}）$．

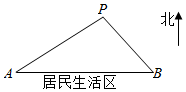如图所示，A，B是两个垃圾中转站，B在A的正东方向16千米处，AB的南面为居民生活区，为了妥善处理生活垃圾，政府决定在AB的背面建一个垃圾发电厂P，垃圾发电厂P的选址拟满足以下两个要求（A，B，P可看成三个点）：
①垃圾发电厂到两个中转站的距离与它们每天集中的生活垃圾量成反比，比例系数相同；
②垃圾发电厂应尽量远离居民区（这里参考的指标是点P到直线AB的距离要尽可能大），现估测得A，B两个中转站每天集中的生活垃圾量分别约为30吨和50吨，设|PA|=5x＞0．
（1）求cos∠PAB（用x的表达式表示）
（2）问垃圾发电厂该如何选址才能同时满足上述要求？

函数$f（x）=Asin（ωx+φ）+b（ω＞0，|φ|＜\frac{π}{2}）$的图象如下，则f（0）+f（1）+f（2）+…+f（2016）=（　　）

2．设a，b是不相等的两个正数，且blna-alnb=a-b，给出下列结论：
①a+b-ab＞1；②a+b＞2；③$\frac{1}{a}$+$\frac{1}{b}$＞2．
其中所有正确结论的序号是①②③．

19．已知复数$z=\frac{1-i}{1+i}$，则z²⁰¹⁶=（　　）

20．盒中共有6件除了颜色外完全相同的产品，其中有1件红色，2件白色和3件黑色，从中任取两件，则两件颜色不相同的概率为（　　）

$\frac{11}{15}$