题目内容
1.将$y=cos({2x+\frac{π}{4}})$的图象向右平移$\frac{π}{4}$个单位,则平移后图象的一个对称中心是( )| A. | $({\frac{3π}{8},0})$ | B. | $({\frac{π}{8},0})$ | C. | $({\frac{3π}{4},0})$ | D. | $({\frac{π}{4},0})$ |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律可得平移后所得函数的解析式,再利用正弦函数的图象的对称性,得出结论.
解答 解:将$y=cos({2x+\frac{π}{4}})$的图象向右平移$\frac{π}{4}$个单位,可得函数y=cos[2(x-$\frac{π}{4}$)+$\frac{π}{4}$]=cos(2x-$\frac{π}{4}$)的图象,
令2x-$\frac{π}{4}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{3π}{8}$,故平移后图象的对称中心为($\frac{kπ}{2}$+$\frac{3π}{8}$,0),k∈Z,
令k=0,可得平移后图象的一个对称中心是($\frac{3π}{8}$,0),
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
12.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{5}$,左、右交点分别为F1,F2,点P在双曲线的右支上,且满足|OP|=|OF2|(O为坐标原点),则|PF1|:|PF2|等于( )
| A. | $\sqrt{2}$:1 | B. | $\sqrt{3}$:1 | C. | 2:1 | D. | $\sqrt{6}$:2 |
16.已知集合M={0,1,2},N={x|x=-a,a∈M},则集合M∪N=( )
| A. | {-2,-1,0,1,0,2} | B. | {0} | C. | {-2,-1,1,2} | D. | {-2,-1,0,1,2} |
6.已知函数f(x=$\left\{\begin{array}{l}{f(x+2),x<2}\\{(\frac{1}{3})^{x},x≥2}\end{array}\right.$,f(-1+log35)的值为( )
| A. | $\frac{1}{15}$ | B. | $\frac{5}{3}$ | C. | 15 | D. | $\frac{2}{3}$ |
13.下列命题:
①“若a≤b,则a<b”的否命题;
②“若a=1,则ax2-x+3≥0的解集为R”的逆否命题;
③“周长相同的圆面积相等”的逆命题;
④“若$\sqrt{2}x$为有理数,则x为无理数”的逆否命题.
其中真命题序号为( )
①“若a≤b,则a<b”的否命题;
②“若a=1,则ax2-x+3≥0的解集为R”的逆否命题;
③“周长相同的圆面积相等”的逆命题;
④“若$\sqrt{2}x$为有理数,则x为无理数”的逆否命题.
其中真命题序号为( )
| A. | ②④ | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
10.设全集U=R,集合A={x|x(x-3)>0},则∁UA=( )
| A. | [0,3] | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-∞,0]∪[3,+∞) |
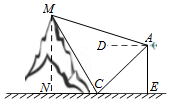 如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m.
如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m.