题目内容

3．设随机变量ξ～N（2，4），若P（ξ＞a+2）=P（ξ＜2a-3），则实数a的值为$\frac{5}{3}$．

分析 直接利用正态分布的对称性，列出方程求解即可．

解答 解：由题意可知随机变量ξ～N（2，4），满足正态分布，对称轴为μ=2，
P（ξ＞a+2）=P（ξ＜2a-3），
则：a+2+2a-3=4，解得a=$\frac{5}{3}$．
故答案为$\frac{5}{3}$．

点评 本题考查正态分布的基本性质的应用，考查计算能力．

练习册系列答案
相关题目
13．已知函数f（x）=（x-1）ex-ax2，若y=f（cosx）在x∈[0，π]上有且仅有两个不同的零点，则实数a的取值范围为a≤-$\frac{2}{e}$．
14．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率e=$\frac{{\sqrt{2}}}{2}$，左顶点为A（-2，0）．
（1）求椭圆E的方程；
（2）已知O为坐标原点，B，C是椭圆E上的两点，连接AB的直线平行OC交y轴于点D，证明：|AB|$，\;\;\sqrt{2}|{OC}|\;\;，\;\;|{AD}$|成等比数列．
11．已知函数$f（x）=xlnx-\frac{a}{2}{x^2}$，直线l：y=（k-2）x-k+1，且k∈Z．
（1）若$?{x_0}∈[{e，{e^2}}]$，使得f（x0）＞0成立，求实数a的取值范围；
（2）设a=0，当x＞1时，函数f（x）的图象恒在直线l的上方，求k的最大值．
18．某几何体的三视图如图所示，它的表面积为（　　）
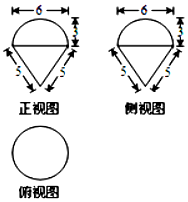
A．66πB．51πC．48πD．33π
8．某电视台曾在某时间段连续播放5个不同的商业广告，现在要在该时间段只保留其中的2个商业广告，新增播一个商业广告与两个不同的公益宣传广告，且要求两个公益宣传广告既不能连续播放也不能在首尾播放，则不同的播放顺序共有（　　）
A．60种B．120种C．144种D．300种
15．已知m，n是两条不同的直线，α，β是两个不重合的平面．命题p：若α∩β=m，m⊥n，则n⊥α；命题q：若m∥α，m?β，α∩β=n，则m∥n．那么下列命题中的真命题是（　　）
A．p∧qB．p∨￢qC．￢p∧qD．￢p∧￢q
5．记关于x的不等式$1-\frac{a}{x}＜0$的解集为P，不等式|x+2|＜3的解集为Q
（1）若a=3，求P；
（2）若P∪Q=Q，求正数a的取值范围．
6．下列命题中为真命题的是③④．
①若两个平面α∥β，a?α，b?β，则a∥b；
②若两个平面α∥β，a?α，b?β，则a与b一定异面；
③若两个平面α∥β，a?α，b?β，则a与b一定不相交；
④若两个平面α∥β，a?α，b?β，则a与b共面或异面；
⑤若两个平面α∥β，a?α，则a与β一定相交．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网