题目内容
6.设$θ∈(0,\frac{π}{2})$,向量$\overrightarrow a=(cosθ,2)$,$\overrightarrow b=(-1,sinθ)$,若$\overrightarrow a⊥\overrightarrow b$,则tanθ=$\frac{1}{2}$.分析 根据两向量垂直时数量积为0,列方程求出tanθ的值.
解答 解:设$θ∈(0,\frac{π}{2})$,向量$\overrightarrow a=(cosθ,2)$,$\overrightarrow b=(-1,sinθ)$,
若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow{a}$•$\overrightarrow{b}$=0
-cosθ+2sinθ=0
∴$\frac{sinθ}{cosθ}$=tanθ=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了平面向量数量积的应用问题,也考查了同角的三角函数关系应用问题,是基础题.

练习册系列答案
相关题目
16.已知集合A={x|x2-2x-3≤0},B={x|x>0},则A∩B=( )
| A. | (0,3] | B. | (0,3) | C. | [0,3] | D. | [3,+∞) |
1.若将函数f(x)=sin2x+cos2x的图象向左平移φ(φ>0)个单位,所得的图象关于y轴对称,则φ的最小值是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{π}{8}$ | D. | $\frac{5π}{8}$ |
18.某几何体的三视图如图所示,它的表面积为( )
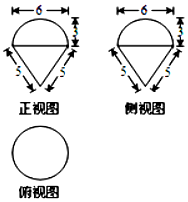

| A. | 66π | B. | 51π | C. | 48π | D. | 33π |
15.已知m,n是两条不同的直线,α,β是两个不重合的平面.命题p:若α∩β=m,m⊥n,则n⊥α;命题q:若m∥α,m?β,α∩β=n,则m∥n.那么下列命题中的真命题是( )
| A. | p∧q | B. | p∨¬q | C. | ¬p∧q | D. | ¬p∧¬q |
 如图,在△AOC中,∠O=90°,∠C=30°,B是边OA上一点,D是边OC上一动点,且当CD=100($\sqrt{3}$-1)时,∠ADO=45°
如图,在△AOC中,∠O=90°,∠C=30°,B是边OA上一点,D是边OC上一动点,且当CD=100($\sqrt{3}$-1)时,∠ADO=45°