题目内容
已知函数f(x)=b•ax(a,b为常数且a>0,a≠1)的图象经过点A(1,8),B(3,32)
(1)试求a,b的值;
(2)若不等式(
)x+(
)x-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
(1)试求a,b的值;
(2)若不等式(
| 1 |
| a |
| 1 |
| b |
考点:指数函数综合题
专题:函数的性质及应用
分析:(1)由函数f(x)=b•ax,(其中a,b为常数且a>0,a≠1)的图象经过点A(1,8),B(3,32),知
,由此能求出f(x).
(2)设g(x)=(
)x+(
)x=(
)x+(
)x,
则y=g(x)在R上是减函数,故当x≤1时,g(x)min=g(1)=
.由此能求出实数m的取值范围.
|
(2)设g(x)=(
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| 1 |
| 4 |
则y=g(x)在R上是减函数,故当x≤1时,g(x)min=g(1)=
| 3 |
| 4 |
解答:
解:(1)∵函数f(x)=b•ax,(其中a,b为常数且a>0,a≠1)的图象经过点A(1,8),B(3,32),
∴
,
解得a=2,b=4,
∴f(x)=4•(2)x=2x+2,
(2)设g(x)=(
)x+(
)x=(
)x+(
)x,
y=g(x)在R上是减函数,
∴当x≤1时,g(x)min=g(1)=
.
若不等式(
)x+(
)x-m≥0在x∈(-∞,1]时恒成立,
即m≤
∴
|
解得a=2,b=4,
∴f(x)=4•(2)x=2x+2,
(2)设g(x)=(
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| 1 |
| 4 |
y=g(x)在R上是减函数,
∴当x≤1时,g(x)min=g(1)=
| 3 |
| 4 |
若不等式(
| 1 |
| a |
| 1 |
| b |
即m≤
| 3 |
| 4 |
点评:本题考查函数解析式的求法,考查满足条件的实数的取值范围的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
已知函数f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有四个不同的实数根,则t的取值范围为( )
A、(-∞,-
| ||
| B、(-∞,-2) | ||
C、(-
| ||
D、(
|
已知a=
,函数f(x)=ax,若实数m,n满足f(m)>f(n),?则m,n的关系为( )
| ||
| 2 |
| A、m+n<0 | B、m+n>0 |
| C、m>n | D、m<n |
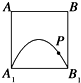
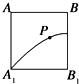
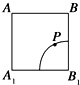
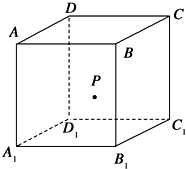 如图正方体A1B1C1D1-ABCD的侧面AB1内有动点P到直线AB与到直线B1C1的距离相等,则动点P所在的曲线的形状为 ( )
如图正方体A1B1C1D1-ABCD的侧面AB1内有动点P到直线AB与到直线B1C1的距离相等,则动点P所在的曲线的形状为 ( )
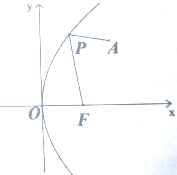 如图,F是抛物线C:y2=2px的焦点,点A(4,2)为抛物线于内一点,点P为抛物线上一动点,|PA|+|PF|的最小值为8
如图,F是抛物线C:y2=2px的焦点,点A(4,2)为抛物线于内一点,点P为抛物线上一动点,|PA|+|PF|的最小值为8