题目内容

7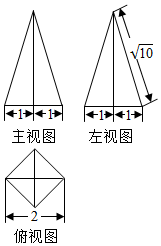．一个四棱锥的底面为正方形，其三视图如图所示，其中主视图和左视图均为等腰三角形，俯视图是一个正方形，则这个四棱锥的体积是（　　）
A．1B．2C．3D．4

分析 根据三视图计算三棱锥的底面积和高，代入体积公式计算．

解答 解：由三视图可知四棱锥底面正方形对角线为2，∴棱锥底面积S=$\frac{1}{2}×{2}^{2}$=2，
由左视图可知棱锥的高h=$\sqrt{10-1}=3$．
∴四棱锥的体积V=$\frac{1}{3}Sh$=$\frac{1}{3}×2×3$=2．
故选：B．

点评 本题考查了棱锥的三视图和结构特征，属于基础题．

练习册系列答案
相关题目
17．函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的最小值为-2，其图象相邻的最高点和最低点的横坐标差是3π，又图象过点（0，1），求：
（1）函数f（x）的解析式；
（2）函数f（x）在区间$[-\frac{3π}{2}，0]$上的最值．
18．已知向量$\overrightarrow a=（{sinωx，cosωx}），\overrightarrow b=（{2sinωx，2\sqrt{3}cosωx}）$，函数$f（x）=\overrightarrow a•\overrightarrow b+λ，（{x∈R}）$的图象关于直线$x=\frac{π}{3}$对称，且经过点$（{\frac{π}{4}，\sqrt{3}}）$，其中ω，λ为实数，ω∈（0，2）．
（1）求f（x）的解析式；
（2）若锐角α，β满足$f（{\frac{α}{2}+\frac{π}{3}}）=\frac{2}{7}，f（{\frac{α+β}{2}+\frac{π}{12}}）=\frac{{5\sqrt{3}}}{7}$，求β的值．
15．如果不等式ax2+bx+c＞0的解集为{x|-2＜x＜4}，那么对于函数f（x）=ax2+bx+c应有（　　）
A．f（5）＜f（2）＜f（-1）B．f（-1）＜f（5）＜f（2）C．f（2）＜f（-1）＜f（5）D．f（5）＜f（-1）＜f（2）
2．函数f（x）=x3-3x+1的单调减区间为（-1，1）．
12．已知函数f（x）=2cos（x+$\frac{5π}{12}$）sin（x+$\frac{π}{4}$）+$\frac{1}{2}$，x∈R．
（1）求f（x）的单调增区间；
（2）已知△ABC内角A、B、C的对边分别为a、b、c，且c=3，f（C）=-$\frac{\sqrt{3}}{2}$，若向量$\overrightarrow{m}$=（1，sinA）与$\overrightarrow{n}$=（2，sinB）共线，求a、b的值．
19．已知θ∈（0，$\frac{π}{2}$），求g（θ）=（$\frac{1}{2}$+cosθ）（$\frac{\sqrt{3}}{2}$+sinθ）的最大值．
16．已知tanθ=2，且θ∈（$\frac{π}{2}$，$\frac{3π}{2}$），则sin$\frac{θ}{2}$=$\frac{\sqrt{50+10\sqrt{5}}}{10}$．
17．已知α∈（π，2π），cosα=$\frac{3\sqrt{10}}{10}$，则tanα等于（　　）
A．2B．-$\frac{1}{3}$C．-$\frac{1}{2}$D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网