题目内容
16.已知tanθ=2,且θ∈($\frac{π}{2}$,$\frac{3π}{2}$),则sin$\frac{θ}{2}$=$\frac{\sqrt{50+10\sqrt{5}}}{10}$.分析 由条件利用同角三角函数的基本关系,二倍角公式即可求出.
解答 解:∵tanθ=2,且θ∈($\frac{π}{2}$,$\frac{3π}{2}$),
∴$\frac{sinθ}{cosθ}$=tanθ=2,
∴sinθ=2cosθ,
∵sin2θ+cos2θ=1,
∴cosθ=-$\frac{\sqrt{5}}{5}$,
∵θ∈($\frac{π}{2}$,$\frac{3π}{2}$),
∴$\frac{θ}{2}$∈($\frac{π}{4}$,$\frac{3π}{4}$),
∴sin2$\frac{θ}{2}$=$\frac{1}{2}$(1-cosθ)=$\frac{1}{2}$×(1+$\frac{\sqrt{5}}{5}$)
∴sin$\frac{θ}{2}$=$\sqrt{\frac{5+\sqrt{5}}{10}}$=$\frac{\sqrt{50+10\sqrt{5}}}{10}$,
故答案为:$\frac{\sqrt{50+10\sqrt{5}}}{10}$
点评 本题考查了同角三角函数的关系和二倍角公式,培养学生的元素能力,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
6.在三棱锥S-ABC中,E,F分别为SB,SC上的点,且EF∥面ABC,则( )
| A. | EF与BC相交 | B. | EF∥BC | C. | EF与BC异面 | D. | 以上均有可能 |
11.已知菱形的两邻边$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,其对角线交点为D,则$\overrightarrow{OD}$等于( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{a}$ | C. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$+$\overrightarrow{b}$ |
1.设D是△ABC的边BC上一点,且$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{DC}$,若AB:AD:AC=3:k:1,则k的取值范围是( )
| A. | ($\frac{1}{3}$,$\frac{4}{3}$) | B. | (1,4) | C. | ($\frac{5}{3}$,$\frac{7}{3}$) | D. | (5,7) |
8.已知在边长为1的正方形ABCD中,E、F分别在线段AB,BC上运动,若EF=1,则$\overrightarrow{EC}$$•\overrightarrow{FD}$的取值范围是( )
| A. | [1-$\sqrt{2}$,0] | B. | [0,$\sqrt{2}$+1] | C. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | D. | [1,$\sqrt{2}$+1] |
20.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)的最小正周期为π,把函数f(x)的图象沿x轴向左平移$\frac{π}{6}$个长度单位,得到函数g(x)的解析式为( )
| A. | g(x)=2sin(2x+$\frac{2π}{3}$) | B. | g(x)=2sin(2x-$\frac{π}{6}$) | C. | g(x)=2sin2x | D. | g(x)=2cos2x |
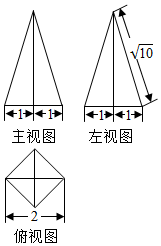 一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )
一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )