题目内容
17.已知α∈(π,2π),cosα=$\frac{3\sqrt{10}}{10}$,则tanα等于( )| A. | 2 | B. | -$\frac{1}{3}$ | C. | -$\frac{1}{2}$ | D. | 3 |
分析 由题意利用同角三角函数的基本关系,求得sinα 的值,可得tanα的值.
解答 解:∵α∈(π,2π),cosα=$\frac{3\sqrt{10}}{10}$,∴α∈($\frac{3π}{2}$,2π),sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{\sqrt{10}}{10}$,
则tanα=$\frac{sinα}{cosα}$=-$\frac{1}{3}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目
8.已知在边长为1的正方形ABCD中,E、F分别在线段AB,BC上运动,若EF=1,则$\overrightarrow{EC}$$•\overrightarrow{FD}$的取值范围是( )
| A. | [1-$\sqrt{2}$,0] | B. | [0,$\sqrt{2}$+1] | C. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | D. | [1,$\sqrt{2}$+1] |
12.α是第四象限角,cosα=$\frac{12}{13}$,则sin(20kπ-α)=( )
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
20.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)的最小正周期为π,把函数f(x)的图象沿x轴向左平移$\frac{π}{6}$个长度单位,得到函数g(x)的解析式为( )
| A. | g(x)=2sin(2x+$\frac{2π}{3}$) | B. | g(x)=2sin(2x-$\frac{π}{6}$) | C. | g(x)=2sin2x | D. | g(x)=2cos2x |
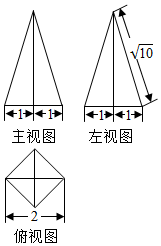 一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )
一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )