题目内容
2.函数f(x)=x3-3x+1的单调减区间为(-1,1).分析 求函数的导函数,令导函数小于零,解此不等式即可求得函数y=x3-3x+1的单调递减区间.
解答 解:令f′(x)=3x2-3<0
解得-1<x<1,
∴函数y=x3-3x的单调递减区间是(-1,1).
故答案为:(-1,1).
点评 本题主要考查了学生利用导数研究函数的单调性,一般步骤是先求定义域,然后令f′(x)>0求出单调增区间,令f′(x)<0求出单调减区间,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
12.已知球的内接三棱锥D一ABC,△ABC中,AB⊥AC且AB=AC=2$\sqrt{2}$,DB=DC=4,二面角A-BC-D的大小为$\frac{3π}{4}$,若球内一飞行物(忽略其大小)可以在球内任意飞行,则落在三棱锥D-ABC内的概率为( )
| A. | $\frac{3π}{13}$ | B. | $\frac{8\sqrt{2}}{27π}$ | C. | $\frac{8}{85π}$ | D. | $\frac{9\sqrt{10}}{200π}$ |
13.某几何体的三视图如图所示,则该几何体的体积是( )
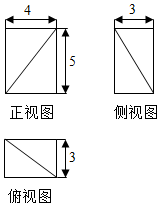

| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
10.已知角α的终边与圆心为原点的圆交于点P(1,2),那么sin2α的值是( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
14.过点P(1,2)且倾斜角是直线x-y-3=0的倾斜角的两倍的直线的方程是( )
| A. | x-2y=0 | B. | x=1 | C. | x-2y-4=0 | D. | y=2 |
11.已知菱形的两邻边$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,其对角线交点为D,则$\overrightarrow{OD}$等于( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{a}$ | C. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$+$\overrightarrow{b}$ |
12.α是第四象限角,cosα=$\frac{12}{13}$,则sin(20kπ-α)=( )
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
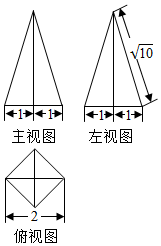 一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )
一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )