题目内容
19.已知θ∈(0,$\frac{π}{2}$),求g(θ)=($\frac{1}{2}$+cosθ)($\frac{\sqrt{3}}{2}$+sinθ)的最大值.分析 化简得出g(θ)=$\frac{1}{2}$sin2θ+sin($θ+\frac{π}{3}$)$+\frac{\sqrt{3}}{4}$,判断不能同时达到最大值,只能够利用导数求解即可.
解答 解:∵g(θ)=$\frac{1}{2}$sin2θ+sin($θ+\frac{π}{3}$)$+\frac{\sqrt{3}}{4}$,
∴g′(θ)=cos2θ$+cos(θ+\frac{π}{3})$,
g′(θ)=0
即cos(2θ)=cos($θ+\frac{4π}{3}$),
∴2θ=$θ+\frac{4}{3}$π,2θ+θ$+\frac{4}{3}$π=2π
即θ=$\frac{4}{3}$π,$θ=\frac{2π}{9}$
∵θ∈(0,$\frac{π}{2}$),
∴$θ=\frac{2π}{9}$,
∴最大值为为:($\frac{1}{2}$+cos$\frac{2π}{9}$)($\frac{\sqrt{3}}{2}$+sin$\frac{2π}{9}$).
点评 本题考查两角和与差的正弦函数,涉及同角三角函数基本关系,属基础题

练习册系列答案
相关题目
10.已知角α的终边与圆心为原点的圆交于点P(1,2),那么sin2α的值是( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
14.过点P(1,2)且倾斜角是直线x-y-3=0的倾斜角的两倍的直线的方程是( )
| A. | x-2y=0 | B. | x=1 | C. | x-2y-4=0 | D. | y=2 |
11.已知菱形的两邻边$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,其对角线交点为D,则$\overrightarrow{OD}$等于( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{a}$ | C. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$+$\overrightarrow{b}$ |
8.已知在边长为1的正方形ABCD中,E、F分别在线段AB,BC上运动,若EF=1,则$\overrightarrow{EC}$$•\overrightarrow{FD}$的取值范围是( )
| A. | [1-$\sqrt{2}$,0] | B. | [0,$\sqrt{2}$+1] | C. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | D. | [1,$\sqrt{2}$+1] |
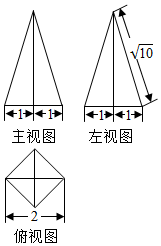 一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )
一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )