题目内容
2.已知△ABC各顶点的坐标分别为(xA,yA),(xB,yB),(xC,yC),点E,F分别在AC、AB上,AE=$\frac{1}{3}$AC,AF=$\frac{1}{4}$AB,BE、CF交于点D,求D点坐标.分析 可作出图形,并连接AD,可由C,D,F三点共线得出$\overrightarrow{AD}=\frac{1-λ}{4}\overrightarrow{AB}+λ\overrightarrow{AC}$,从而同理得出$\overrightarrow{AD}=\frac{1-μ}{3}\overrightarrow{AC}+μ\overrightarrow{AB}$,这样根据平面向量基本定理即可得出关于λ,μ的二元一次方程组,可解出$μ=\frac{2}{11}$,从而有$\overrightarrow{AD}=\frac{3}{11}\overrightarrow{AC}+\frac{2}{11}\overrightarrow{AB}$.可设D(x,y),从而可以写出$\overrightarrow{AD},\overrightarrow{AC},\overrightarrow{AB}$的坐标,进行向量坐标的数乘和加法运算即可求出$\overrightarrow{AD}$坐标,根据坐标相等便可分别建立关于x,y的一元一次方程,从而可解出x,y,这样便可得出D点的坐标.
解答 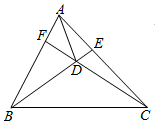 解:如图,连接AD;
解:如图,连接AD;
∵C,D,F三点共线;
∴$\overrightarrow{AD}=(1-λ)\overrightarrow{AF}+λ\overrightarrow{AC}$=$\frac{1-λ}{4}\overrightarrow{AB}+λ\overrightarrow{AC}$;
同理由B,D,E三点共线得:$\overrightarrow{AD}=\frac{1-μ}{3}\overrightarrow{AC}+μ\overrightarrow{AB}$;
∴$\left\{\begin{array}{l}{λ=\frac{1-μ}{3}}\\{\frac{1-λ}{4}=μ}\end{array}\right.$;
$μ=\frac{2}{11}$;
∴$\overrightarrow{AD}=\frac{3}{11}\overrightarrow{AC}+\frac{2}{11}\overrightarrow{AB}$;
设D(x,y),$\overrightarrow{AD}=(x-{x}_{A},y-{y}_{A}),\overrightarrow{AC}=({x}_{c}-{x}_{A},{y}_{c}-{y}_{A})$,$\overrightarrow{AB}=({x}_{B}-{x}_{A},{y}_{B}-{y}_{A})$;
∴(x-xA,y-yA)=$(\frac{3{x}_{C}+2{x}_{B}-5{x}_{A}}{11},\frac{3{y}_{C}+2{y}_{B}-5{y}_{A}}{11})$;
∴$\left\{\begin{array}{l}{x-{x}_{A}=\frac{3{x}_{C}+2{x}_{B}-5{x}_{A}}{11}}\\{y-{y}_{A}=\frac{3{y}_{C}+2{y}_{B}-5{y}_{A}}{11}}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=\frac{3{x}_{C}+2{x}_{B}+6{x}_{A}}{11}}\\{y=\frac{3{y}_{C}+2{y}_{B}+6{y}_{A}}{11}}\end{array}\right.$;
∴D点的坐标为$(\frac{3{x}_{C}+2{x}_{B}+6{x}_{A}}{11},\frac{3{y}_{C}+2{y}_{B}+6{y}_{A}}{11})$.
点评 考查三点A,B,C共线时,便可得到$\overrightarrow{OB}=(1-k)\overrightarrow{OA}+k\overrightarrow{OC}$,根据点的坐标可求向量的坐标,向量坐标的加法和数乘运算,以及平面向量基本定理.

 阅读快车系列答案
阅读快车系列答案| 使用寿命 | [500,700) | [700,900) | [900,1100) | [1100,1300) | [1300,1500] |
| 只数 | 5 | 23 | 44 | 25 | 3 |
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
| A. | {-1,0} | B. | {0,1,2} | C. | {-1,0,1} | D. | {-2,-1,0} |
 如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点.
如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点.