题目内容
已知函数f(x)=
x2+ax-2a2lnx(其中a为实数).
(1)若函数f(x)在x=1处取得极小值,求a的值;
(2)若对于任意的x∈(0,1],都有f(x)≥0成立,求实数a的取值范围.
| 1 |
| 2 |
(1)若函数f(x)在x=1处取得极小值,求a的值;
(2)若对于任意的x∈(0,1],都有f(x)≥0成立,求实数a的取值范围.
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)由已知得f′(x)=x+a-
,f′(1)=1+a-2a2=0,由此能求出a.
(2)由f′(x)=x+a-
=0,得x=a,或x=-2a,由此利用分类讨论思想和导数性质能求出实数a的取值范围.
| 2a2 |
| x |
(2)由f′(x)=x+a-
| 2a2 |
| x |
解答:
解:(1)∵f(x)=
x2+ax-2a2lnx,
∴f′(x)=x+a-
,
∵函数f(x)在x=1处取得极小值,
∴f′(1)=1+a-2a2=0,
解得a=-
或a=1.
(2)由f′(x)=x+a-
=0,
得x=a,或x=-2a,
①x∈(0,1],当a>0时,
x∈(a,+∞],f′(x)>0;x∈(0,a),f′(x)<0,
∴f(x)最小值=f(a)=
a2+a2-2a2lna=
a2-2a2lna,
∵对于任意的x∈(0,1],都有f(x)≥0成立,
∴f(x)最小值=
a2-2a2lna≥0,
∴0<a≤e
;
②x∈(0,1],当a=0时,
f(x)=
x2对于任意的x∈(0,1],都有f(x)≥0成立,
∴a=0成立;
③x∈(0,1],当a<0时,
x∈(-2a,+∞],f′(x)>0;x∈(0,-2a),f′(x)<0,
f(x)最小值=f(-2a)=2a2-2a2-2a2ln(-2a)=-2a2ln(-2a),
∵对于任意的x∈(0,1],都有f(x)≥0成立,
∴f(x)最小值=-2a2ln(-2a)≥0,
解得a≥-
.
综上,实数a的取值范围是[-
,e
].
| 1 |
| 2 |
∴f′(x)=x+a-
| 2a2 |
| x |
∵函数f(x)在x=1处取得极小值,
∴f′(1)=1+a-2a2=0,
解得a=-
| 1 |
| 2 |
(2)由f′(x)=x+a-
| 2a2 |
| x |
得x=a,或x=-2a,
①x∈(0,1],当a>0时,
x∈(a,+∞],f′(x)>0;x∈(0,a),f′(x)<0,
∴f(x)最小值=f(a)=
| 1 |
| 2 |
| 3 |
| 2 |
∵对于任意的x∈(0,1],都有f(x)≥0成立,
∴f(x)最小值=
| 3 |
| 2 |
∴0<a≤e
| 3 |
| 4 |
②x∈(0,1],当a=0时,
f(x)=
| 1 |
| 2 |
∴a=0成立;
③x∈(0,1],当a<0时,
x∈(-2a,+∞],f′(x)>0;x∈(0,-2a),f′(x)<0,
f(x)最小值=f(-2a)=2a2-2a2-2a2ln(-2a)=-2a2ln(-2a),
∵对于任意的x∈(0,1],都有f(x)≥0成立,
∴f(x)最小值=-2a2ln(-2a)≥0,
解得a≥-
| 1 |
| 2 |
综上,实数a的取值范围是[-
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力.解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
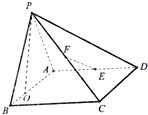 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD、PC的中点.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD、PC的中点.