题目内容
已知椭圆
+
=1与抛物线y2=2px(p>0)有公共焦点F(c,0)(c∈N*),M是它们的一个交点,S△MOF=2
,且|MF|=5.
(1)求椭圆及抛物线的方程;
(2)是否存在过F的直线l被椭圆及抛物线截得的弦长相等,若存在,求出l的方程;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
(1)求椭圆及抛物线的方程;
(2)是否存在过F的直线l被椭圆及抛物线截得的弦长相等,若存在,求出l的方程;若不存在,说明理由.
考点:椭圆的简单性质
专题:计算题,存在型,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)求出抛物线的焦点,准线方程,运用抛物线的定义得到M的横坐标,再由面积公式,得到M的纵坐标,代入抛物线方程,即可解得,p=4,进而得到a,b,c,得到椭圆方程和抛物线方程;
(2)设出直线l的方程,联立抛物线方程和椭圆方程,消去y,得到x的方程,运用韦达定理和弦长公式,列出等式,解得即可.
(2)设出直线l的方程,联立抛物线方程和椭圆方程,消去y,得到x的方程,运用韦达定理和弦长公式,列出等式,解得即可.
解答:
解:(1)抛物线y2=2px(p>0)的焦点(
,0),
准线方程x=-
,则由抛物线的定义,可得,|MF|=xM+
=5,
即有xM=5-
,设M在第一象限,
又S△MOF=2
,则有
•
•yM=2
.
即有yM=
,再代入抛物线方程,可得,
=10p-p2,(由于c∈N*,则p为偶数),
解得,p=4.则有c=2,M(3,2
),
即有a2-b2=4,
+
=1.
解得,a2=36,b2=32.
则椭圆方程为:
+
=1,抛物线方程为:y2=8x;
(2)假设存在过F的直线l被椭圆及抛物线截得的弦长相等.
则设直线l:y=k(x-2),代入抛物线方程,得到,
k2x2-(4k2+8)x+4k2=0,设交点的横坐标为x1,x2,
则有x1+x2=
,
由抛物线的定义可得,弦长为:x1+x2+4=8+
,
联立椭圆方程,消去y,得,(8+9k2)x2-36k2x+36k2-288=0,
设交点的横坐标为x3,x4,则x3+x4=
,
由椭圆的第二定义可得,弦长为:a-ex3+a-ex4=2a-e(x3+x4)
=12-
•
=
由8+
=
,解得,k2=
,解得,k=±
.
则存在过F的直线l:y=±
(x-2),被椭圆及抛物线截得的弦长相等.
| p |
| 2 |
准线方程x=-
| p |
| 2 |
| p |
| 2 |
即有xM=5-
| p |
| 2 |
又S△MOF=2
| 6 |
| 1 |
| 2 |
| p |
| 2 |
| 6 |
即有yM=
8
| ||
| p |
| 384 |
| p2 |
解得,p=4.则有c=2,M(3,2
| 6 |
即有a2-b2=4,
| 9 |
| a2 |
| 24 |
| b2 |
解得,a2=36,b2=32.
则椭圆方程为:
| x2 |
| 36 |
| y2 |
| 32 |
(2)假设存在过F的直线l被椭圆及抛物线截得的弦长相等.
则设直线l:y=k(x-2),代入抛物线方程,得到,
k2x2-(4k2+8)x+4k2=0,设交点的横坐标为x1,x2,
则有x1+x2=
| 4k2+8 |
| k2 |
由抛物线的定义可得,弦长为:x1+x2+4=8+
| 8 |
| k2 |
联立椭圆方程,消去y,得,(8+9k2)x2-36k2x+36k2-288=0,
设交点的横坐标为x3,x4,则x3+x4=
| 36k2 |
| 8+9k2 |
由椭圆的第二定义可得,弦长为:a-ex3+a-ex4=2a-e(x3+x4)
=12-
| 1 |
| 3 |
| 36k2 |
| 8+9k2 |
| 96+96k2 |
| 8+9k2 |
由8+
| 8 |
| k2 |
| 96+96k2 |
| 8+9k2 |
| 8 |
| 3 |
2
| ||
| 3 |
则存在过F的直线l:y=±
2
| ||
| 3 |
点评:本题考查椭圆和抛物线的方程和定义及性质,考查联立直线方程和抛物线方程、椭圆方程消去未知数,运用韦达定理和弦长公式,考查运算能力,属于中档题.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
把函数y=cos2x+3的图象沿向量
平移后得到函数y=sin(2x-
)的图象,则向量
是( )
| a |
| π |
| 6 |
| a |
A、(
| ||
B、(
| ||
C、(
| ||
D、(-
|
以正方形的一边为轴建立平面直角坐标系,若其直观图是有一条边长为4的平行四边形,则此四边形的面积是( )
| A、16 | B、16或64 |
| C、64 | D、以上都不对 |
在△ABC中,边BC上的高AD=4,则(
-
)•
的值等于( )
| AB |
| AC |
| AD |
| A、0 | B、4 | C、8 | D、12 |
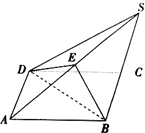 如图所示,四边形ABCD是平行四边形,直线SC⊥平面ABCD,E是SA的中点,求证:平面BDE⊥平面ABCD.
如图所示,四边形ABCD是平行四边形,直线SC⊥平面ABCD,E是SA的中点,求证:平面BDE⊥平面ABCD.