题目内容
把函数y=cos2x+3的图象沿向量
平移后得到函数y=sin（2x-
）的图象，则向量
是（ ）
| a |
| π |
| 6 |
| a |
A、（
| ||
B、（
| ||
C、（
| ||
D、（-
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：先根据诱导公式进行化简，再由左加右减上加下减的原则可确定函数y=cos2x+3到y=sin（2x-
）的路线，进而确定向量
．
| π |
| 6 |
| a |
解答：
解：∵y=cos2x+3=3+sin（2x+
）
设将函数y=3+sin（2x+
）向右平移个φ单位，再向下平移3个单位可得到y=sin（2x-
）的图象，
∴有y=3+sin[2（x-φ）+
]=sin（2x-
）+3，可解得φ=
∴
=（
，-3）
故选：A．
| π |
| 2 |
设将函数y=3+sin（2x+
| π |
| 2 |
| π |
| 6 |
∴有y=3+sin[2（x-φ）+
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴
| a |
| π |
| 3 |
故选：A．
点评：本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减，注意三角函数的化简．
练习册系列答案
口算能手系列答案
相关题目
已知椭圆
+
=1的右焦点是双曲线
-
=1的右顶点，则双曲线的渐近线为（ ）
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| a2 |
| y2 |
| 9 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
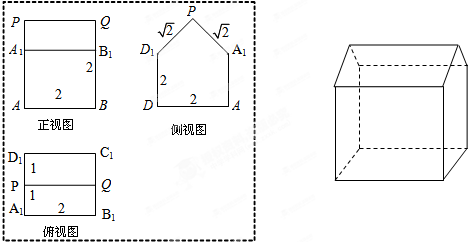
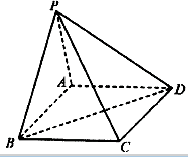如图，在四棱锥P-ABCD中，底面ABCD是正方形，已知AB=2，PA=2，PD=2