题目内容
已知Sn是正项数列{an}的前n项和,4Sn=(an+1)2.
(1)求Sn.
(2)设数列{bn}满足bn=
,数列{bn}的前n项和为Tn,若不等式λTn<n+8对于任意n∈N*恒成立,试求λ的取值范围.
(3)设dn=
,是否存在正整数m,n,且1<m<n,使的d1,dm,dn成等比数列?若存在,求出m,n的值,若不存在,请说明理由.
(1)求Sn.
(2)设数列{bn}满足bn=
| 2 |
| 4Sn-1 |
(3)设dn=
| ||
3
|
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)由已知利用“n=1时,a1=S1;n≥2时,an=Sn-Sn-1”即可得出an,进而得到Sn;
(2)求出等差数列{an}的前n项和,代入bn=
整理,由裂项相消法求出数列{bn}的前n项和为Tn,代入不等式λTn<n+8后分离变量λ,利用基本不等式求出最小值后求得λ的范围;
(3)把Sn代入dn=
,化简后得到dn,结合d1,dm,dn成等比数列得到关于m的不等式,进一步求得m的值,则n的值可求.
(2)求出等差数列{an}的前n项和,代入bn=
| 2 |
| 4Sn-1 |
(3)把Sn代入dn=
| ||
3
|
解答:
解:(1)∵4Sn=(an+1)2,n∈N*,∴4Sn-1=(an-1+1)2(n≥2),
两式作差得4an=(an+1)2-(an-1+1)2,化为(an+an-1)(an-an-1-2)=0,
又∵正项数列{an},∴an+an-1≠0,
∴an-an-1=2(n≥2),
又n=1时,4a1=4S1=(a1+1)2,
解得a1=1,
∴数列{an}是以1为首项,2为公差的等差数列.
∴an=2n-1.
∴Sn=n+
=n2;
(2)bn=
=
=
=
-
,
Tn=(1-
)+(
-
)+…+(
-
)=1-
=
.
由λTn<n+8对于任意n∈N*恒成立,得λ•
<n+8对于任意n∈N*恒成立,
即λ<
=
=2n+
+17.
∵2n+
+17≥2
+17=25(当且仅当n=2时取等号),
∴λ<25;
(3)dn=
=
=
,
假设存在正整数m,n,且1<m<n,使的d1,dm,dn成等比数列,
即dm2=d1dn,也就是(
)2=
•
,
即
=
,
由
=
,得
=
,
则-3m2+6m+1>0,解得
<m<
.
∵m为大于1 的整数,∴m=2.
则n=16.
故存在m=2,n=16,使得d1,dm,dn成等比数列.
两式作差得4an=(an+1)2-(an-1+1)2,化为(an+an-1)(an-an-1-2)=0,
又∵正项数列{an},∴an+an-1≠0,
∴an-an-1=2(n≥2),
又n=1时,4a1=4S1=(a1+1)2,
解得a1=1,
∴数列{an}是以1为首项,2为公差的等差数列.
∴an=2n-1.
∴Sn=n+
| 2n(n-1) |
| 2 |
(2)bn=
| 2 |
| 4Sn-1 |
| 2 |
| 4n2-1 |
| 2 |
| (2n-1)(2n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
Tn=(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+1 |
| 2n |
| 2n+1 |
由λTn<n+8对于任意n∈N*恒成立,得λ•
| 2n |
| 2n+1 |
即λ<
| (2n+1)(n+8) |
| 2n |
| 2n2+17n+8 |
| n |
| 8 |
| n |
∵2n+
| 8 |
| n |
2n•
|
∴λ<25;
(3)dn=
| ||
3
|
| ||
3
|
| n |
| 3n+1 |
假设存在正整数m,n,且1<m<n,使的d1,dm,dn成等比数列,
即dm2=d1dn,也就是(
| m |
| 3m+1 |
| 1 |
| 4 |
| n |
| 3n+1 |
即
| m2 |
| 9m2+6m+1 |
| n |
| 12n+4 |
由
| m2 |
| 9m2+6m+1 |
| n |
| 12n+4 |
| 4 |
| n |
| -3m2+6m+1 |
| m2 |
则-3m2+6m+1>0,解得
3-2
| ||
| 3 |
3+2
| ||
| 3 |
∵m为大于1 的整数,∴m=2.
则n=16.
故存在m=2,n=16,使得d1,dm,dn成等比数列.
点评:本题考查了数列递推式,考查了等差关系的确定,考查了数列的函数特性,训练了由等比数列的性质结合数列的函数特性求解参数问题,属于难题.

练习册系列答案
相关题目
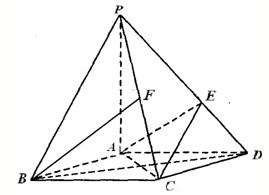 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=